Images 2D

Load the geometrical object from a binary 2D image

In this example, we will:

• Read a 2D binary image from a binary file (for a 3D image volume see Images 3D)
• Build a 2D cartesian OpenFPM grid with same dimensions as the image (1 particle for each pixel in x and y) or refined by arbitrary factor in dimension of choice (e.g. to get a isotropic grid)
• Assign pixel value to a grid node property
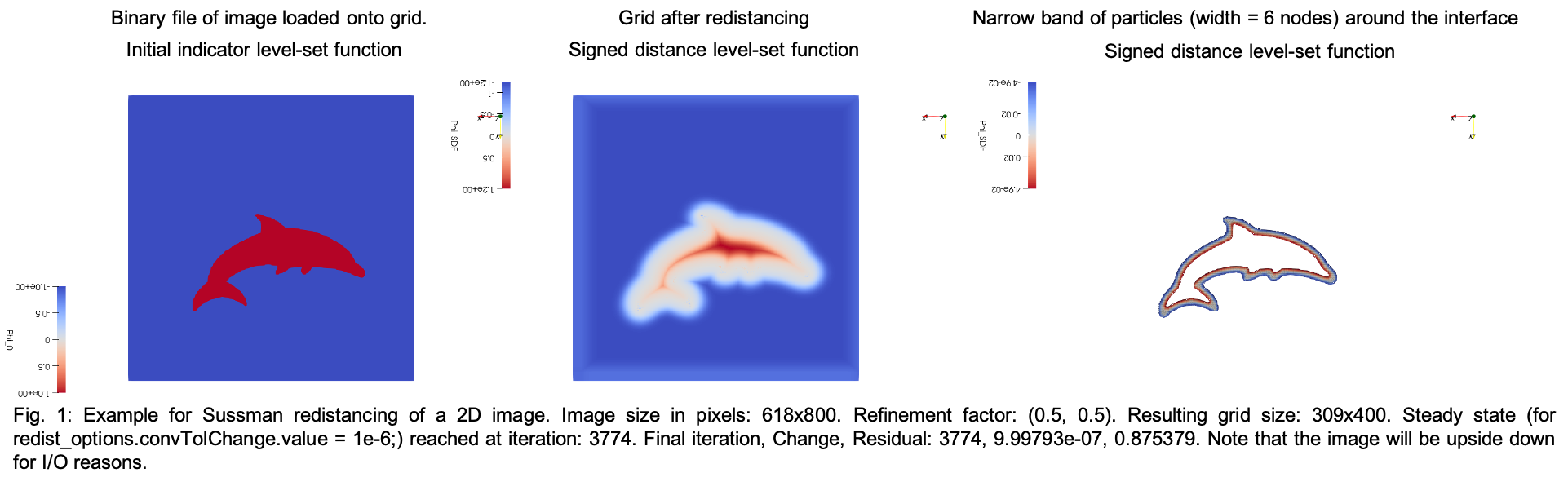
• Run the Sussman Redistancing and get the narrow band around the interface (see also: Disk 2D and example_sussman_sphere)

Output: print on promt : Iteration, Change, Residual (see: DistFromSol::change, DistFromSol::residual) writes vtk and hdf5 files of: 1.) 2D grid with geometrical object pre-redistancing and post-redistancing (Phi_0 and Phi_SDF, respectively) 2.) particles on narrow band around interface.

Visualization of example output in Paraview

Include

These are the header files that we need to include:

 
// Include redistancing header files
#include "util/PathsAndFiles.hpp"
#include "level_set/redistancing_Sussman/RedistancingSussman.hpp"
#include "level_set/redistancing_Sussman/NarrowBand.hpp"
#include "RawReader/InitGridWithPixel.hpp"

Initialization, indices and output folder

Again we start with

• Initializing OpenFPM
• Setting the output path and creating an output folder This time, we also set the input path and name of the binary image that we want to load onto the grid. For this example we provide 3 simple example images. The original (e.g. tiff) image has been converted into -1 / +1 values. A jupyter notebook that does this can be found here: image2binary_dolphin.ipynb. Optionally, we can define the grid dimensionality and some indices for better code readability later on.
• x: First dimension
• y: Second dimension
• Phi_0_grid: Index of property that stores the initial level-set-function
• Phi_SDF_grid: Index of property where the redistancing result should be written to

 
int main(int argc, char* argv[])
{
//  std::string image_name = "circle";
//  std::string image_name = "triangle";
//  std::string image_name = "face";
    std::string image_name = "dolphin";
    
    typedef double phi_type;
    //  initialize library
    openfpm_init(&argc, &argv);
    // Set current working directory, define output paths and create folders where output will be saved
    std::string cwd                     = get_cwd();
    const std::string path_output       = cwd + "/output_" + image_name;
//  const std::string path_output       = cwd + "/output_face";
    
    create_directory_if_not_exist(path_output);
    
    // Now we set the input paths. We need a binary file with the pixel values and a csv file with the
    // size of the stack (in #pixels / dimension)
    const std::string path_input        ="input/";
    const std::string path_to_image     = path_input + image_name + ".bin";
    const std::string path_to_size      = path_input + "size_" + image_name + ".csv";
    
    /*
     * in case of 2D (single image):
     */
    const unsigned int grid_dim         = 2;
    // some indices
    const size_t x                      = 0;
    const size_t y                      = 1;
    
    const size_t Phi_0_grid             = 0;
    const size_t Phi_SDF_grid           = 1;
    
    const size_t Phi_SDF_vd             = 0;
    const size_t Phi_grad_vd            = 1;
    const size_t Phi_magnOfGrad_vd      = 2;

Set refinement factor

If we want that the grid has a different resolution as the image, we can set a refinement factor. In the refinement array, we define by which factor the grid resolution should be changed w.r.t. the image resolution. This can be useful for example when you want to have an isotropic grid but the underlying image is anisotropic (as it often happens for microcsopic z-stacks rather than 2D images).

    const phi_type refinement []          = {0.5, 0.5};   // (2D) factor by which grid should be finer / coarser as
    // underlying image in each dimension (e.g. to get isotropic grid from anisotropic image resolution)

Get size from image_size.csv

Here we read the image size (number of pixel values per dimension) from a csv file. Alternatively, you can directly define the image size as: std::vector<size_t> stack_size {pixels in x, pixels in y}. We use this image size and the refinement factor to set the grid size sz.

    std::vector<int> stack_size = get_size(path_to_size);
    auto & v_cl = create_vcluster();
    if (v_cl.rank() == 0)
    {
        for(std::vector<int>::size_type i = 0; i != stack_size.size(); i++)
        {
            std::cout << "#Pixel in dimension " << i << " = " << stack_size[i] << std::endl;
            std::cout << "original refinement in dimension " << i << " = " << refinement[i] << std::endl;
        }
    }
    
    //  Array with grid dimensions after refinement. This size-array will be used for the grid creation.
    const size_t sz[grid_dim] = {(size_t)std::round(stack_size[x] * refinement[x]), (size_t)std::round(stack_size[y] *
                                                                                                               refinement[y])}; // 2D

Run Sussman redistancing and get narrow band

Once we have loaded the geometrical object from the 2D image onto the grid, we can perform Sussman redistancing and get the narrow band the same way as it is explained in detail here: Disk 2D and here: Sphere 3D.

    Box<grid_dim, phi_type> box({0.0, 0.0}, {5.0, 5.0}); // 2D
    
    Ghost<grid_dim, long int> ghost(0);
    typedef aggregate<phi_type, phi_type> props;
    typedef grid_dist_id<grid_dim, phi_type, props > grid_in_type;
    grid_in_type g_dist(sz, box, ghost);
    g_dist.setPropNames({"Phi_0", "Phi_SDF"});
    
    // initialize complete grid including ghost layer with -1
    init_grid_and_ghost<Phi_0_grid>(g_dist, -1.0);
    
    // Now we can initialize the grid with the pixel values from the image stack
    load_pixel_onto_grid<Phi_0_grid>(g_dist, path_to_image, stack_size);
    g_dist.write(path_output + "/grid_from_images_initial", FORMAT_BINARY); // Save the initial grid as vtk file
    
    
    // Now we want to convert the initial Phi into a signed distance function (SDF) with magnitude of gradient = 1
    // For the initial re-distancing we use the Sussman method
    // 1.) Set some redistancing options (for details see example sussman disk or sphere)
    Redist_options<phi_type> redist_options;
    redist_options.min_iter                             = 1e3;
    redist_options.max_iter                             = 1e4;
    
    redist_options.convTolChange.value                  = 1e-7;
    redist_options.convTolChange.check                  = true;
    redist_options.convTolResidual.value                = 1e-6; // is ignored if convTolResidual.check = false;
    redist_options.convTolResidual.check                = false;
    
    redist_options.interval_check_convergence           = 1e3;
    redist_options.width_NB_in_grid_points              = 10;
    redist_options.print_current_iterChangeResidual     = true;
    redist_options.print_steadyState_iter               = true;
    redist_options.save_temp_grid                       = true;
    
    RedistancingSussman<grid_in_type, phi_type> redist_obj(g_dist, redist_options);   // Instantiation of Sussman-redistancing
    // class
//  std::cout << "dt = " << redist_obj.get_time_step() << std::endl;
    // Run the redistancing. in the <> brackets provide property-index where 1.) your initial Phi is stored and 2.) where the resulting SDF should be written to.
    redist_obj.run_redistancing<Phi_0_grid, Phi_SDF_grid>();
    
    g_dist.write(path_output + "/grid_images_post_redistancing", FORMAT_BINARY); // Save the result as vtk file
    
    //  Get narrow band: Place particles on interface (narrow band width e.g. 2 grid points on each side of the interface)
    size_t bc[grid_dim] = {NON_PERIODIC, NON_PERIODIC};
    // Create an empty vector to which narrow-band particles will be added. You can choose, how many properties you want.
    // Minimum is 1 property, to which the Phi_SDF can be written
    // In this example we chose 3 properties. The 1st for the Phi_SDF, the 2nd for the gradient of phi and the 3rd for
    // the magnitude of the gradient
    typedef aggregate<phi_type, Point<grid_dim, phi_type>, phi_type> props_nb;
    typedef vector_dist<grid_dim, phi_type, props_nb> vd_type;
    Ghost<grid_dim, phi_type> ghost_vd(0);
    vd_type vd_narrow_band(0, box, bc, ghost_vd);
    vd_narrow_band.setPropNames({"Phi_SDF", "Phi_grad", "Phi_magnOfGrad"});
    
    NarrowBand<grid_in_type, phi_type> narrowBand(g_dist, redist_options.width_NB_in_grid_points); // Instantiation of
    // NarrowBand class
    
    // Get the narrow band. You can decide, if you only want the Phi_SDF saved to your particles or
    // if you also want the gradients or gradients and magnitude of gradient.
    // The function will know depending on how many property-indices you provide in the <> brackets.
    // First property-index must always be the index of the SDF on the grid!
    // E.g.: The following line would only write only the Phi_SDF from the grid to your narrow-band particles
    // narrowBand.get_narrow_band<Phi_SDF_grid, Phi_SDF_vd>(g_dist, vd_narrow_band);
    // Whereas this will give you the gradients and magnOfGrad of Phi as well:
    narrowBand.get_narrow_band<Phi_SDF_grid, Phi_SDF_vd, Phi_grad_vd, Phi_magnOfGrad_vd>(g_dist, vd_narrow_band);
    
    vd_narrow_band.write(path_output + "/vd_narrow_band_images", FORMAT_BINARY); // Save particles as vtk file
    
    openfpm_finalize(); // Finalize openFPM library
    return 0;
}

Full code

//
// Created by jstark on 2020-05-18. Updated on 2022-01-05.
//
 
 
// Include redistancing header files
#include "util/PathsAndFiles.hpp"
#include "level_set/redistancing_Sussman/RedistancingSussman.hpp"
#include "level_set/redistancing_Sussman/NarrowBand.hpp"
#include "RawReader/InitGridWithPixel.hpp"
 
 
 
int main(int argc, char* argv[])
{
//  std::string image_name = "circle";
//  std::string image_name = "triangle";
//  std::string image_name = "face";
    std::string image_name = "dolphin";
    
    typedef double phi_type;
    //  initialize library
    openfpm_init(&argc, &argv);
    // Set current working directory, define output paths and create folders where output will be saved
    std::string cwd                     = get_cwd();
    const std::string path_output       = cwd + "/output_" + image_name;
//  const std::string path_output       = cwd + "/output_face";
    
    create_directory_if_not_exist(path_output);
    
    // Now we set the input paths. We need a binary file with the pixel values and a csv file with the
    // size of the stack (in #pixels / dimension)
    const std::string path_input        ="input/";
    const std::string path_to_image     = path_input + image_name + ".bin";
    const std::string path_to_size      = path_input + "size_" + image_name + ".csv";
    
    /*
     * in case of 2D (single image):
     */
    const unsigned int grid_dim         = 2;
    // some indices
    const size_t x                      = 0;
    const size_t y                      = 1;
    
    const size_t Phi_0_grid             = 0;
    const size_t Phi_SDF_grid           = 1;
    
    const size_t Phi_SDF_vd             = 0;
    const size_t Phi_grad_vd            = 1;
    const size_t Phi_magnOfGrad_vd      = 2;
    
    
    const phi_type refinement []          = {0.5, 0.5};   // (2D) factor by which grid should be finer / coarser as
    // underlying image in each dimension (e.g. to get isotropic grid from anisotropic image resolution)
    //  read the stack size (number of pixel values per dimension) from a binary file
    // alternatively, you can directly define the stack size as: std::vector<size_t> stack_size {#pixels in x, #pixels in y}
 
    std::vector<int> stack_size = get_size(path_to_size);
    auto & v_cl = create_vcluster();
    if (v_cl.rank() == 0)
    {
        for(std::vector<int>::size_type i = 0; i != stack_size.size(); i++)
        {
            std::cout << "#Pixel in dimension " << i << " = " << stack_size[i] << std::endl;
            std::cout << "original refinement in dimension " << i << " = " << refinement[i] << std::endl;
        }
    }
    
    //  Array with grid dimensions after refinement. This size-array will be used for the grid creation.
    const size_t sz[grid_dim] = {(size_t)std::round(stack_size[x] * refinement[x]), (size_t)std::round(stack_size[y] *
                                                                                                               refinement[y])}; // 2D
    // Here we create a 2D grid that stores 2 properties:
    // Prop1: store the initial Phi;
    // Prop2: here the re-initialized Phi (signed distance function) will be written to in the re-distancing step
 
    Box<grid_dim, phi_type> box({0.0, 0.0}, {5.0, 5.0}); // 2D
    
    Ghost<grid_dim, long int> ghost(0);
    typedef aggregate<phi_type, phi_type> props;
    typedef grid_dist_id<grid_dim, phi_type, props > grid_in_type;
    grid_in_type g_dist(sz, box, ghost);
    g_dist.setPropNames({"Phi_0", "Phi_SDF"});
    
    // initialize complete grid including ghost layer with -1
    init_grid_and_ghost<Phi_0_grid>(g_dist, -1.0);
    
    // Now we can initialize the grid with the pixel values from the image stack
    load_pixel_onto_grid<Phi_0_grid>(g_dist, path_to_image, stack_size);
    g_dist.write(path_output + "/grid_from_images_initial", FORMAT_BINARY); // Save the initial grid as vtk file
    
    
    // Now we want to convert the initial Phi into a signed distance function (SDF) with magnitude of gradient = 1
    // For the initial re-distancing we use the Sussman method
    // 1.) Set some redistancing options (for details see example sussman disk or sphere)
    Redist_options<phi_type> redist_options;
    redist_options.min_iter                             = 1e3;
    redist_options.max_iter                             = 1e4;
    
    redist_options.convTolChange.value                  = 1e-7;
    redist_options.convTolChange.check                  = true;
    redist_options.convTolResidual.value                = 1e-6; // is ignored if convTolResidual.check = false;
    redist_options.convTolResidual.check                = false;
    
    redist_options.interval_check_convergence           = 1e3;
    redist_options.width_NB_in_grid_points              = 10;
    redist_options.print_current_iterChangeResidual     = true;
    redist_options.print_steadyState_iter               = true;
    redist_options.save_temp_grid                       = true;
    
    RedistancingSussman<grid_in_type, phi_type> redist_obj(g_dist, redist_options);   // Instantiation of Sussman-redistancing
    // class
//  std::cout << "dt = " << redist_obj.get_time_step() << std::endl;
    // Run the redistancing. in the <> brackets provide property-index where 1.) your initial Phi is stored and 2.) where the resulting SDF should be written to.
    redist_obj.run_redistancing<Phi_0_grid, Phi_SDF_grid>();
    
    g_dist.write(path_output + "/grid_images_post_redistancing", FORMAT_BINARY); // Save the result as vtk file
    
    //  Get narrow band: Place particles on interface (narrow band width e.g. 2 grid points on each side of the interface)
    size_t bc[grid_dim] = {NON_PERIODIC, NON_PERIODIC};
    // Create an empty vector to which narrow-band particles will be added. You can choose, how many properties you want.
    // Minimum is 1 property, to which the Phi_SDF can be written
    // In this example we chose 3 properties. The 1st for the Phi_SDF, the 2nd for the gradient of phi and the 3rd for
    // the magnitude of the gradient
    typedef aggregate<phi_type, Point<grid_dim, phi_type>, phi_type> props_nb;
    typedef vector_dist<grid_dim, phi_type, props_nb> vd_type;
    Ghost<grid_dim, phi_type> ghost_vd(0);
    vd_type vd_narrow_band(0, box, bc, ghost_vd);
    vd_narrow_band.setPropNames({"Phi_SDF", "Phi_grad", "Phi_magnOfGrad"});
    
    NarrowBand<grid_in_type, phi_type> narrowBand(g_dist, redist_options.width_NB_in_grid_points); // Instantiation of
    // NarrowBand class
    
    // Get the narrow band. You can decide, if you only want the Phi_SDF saved to your particles or
    // if you also want the gradients or gradients and magnitude of gradient.
    // The function will know depending on how many property-indices you provide in the <> brackets.
    // First property-index must always be the index of the SDF on the grid!
    // E.g.: The following line would only write only the Phi_SDF from the grid to your narrow-band particles
    // narrowBand.get_narrow_band<Phi_SDF_grid, Phi_SDF_vd>(g_dist, vd_narrow_band);
    // Whereas this will give you the gradients and magnOfGrad of Phi as well:
    narrowBand.get_narrow_band<Phi_SDF_grid, Phi_SDF_vd, Phi_grad_vd, Phi_magnOfGrad_vd>(g_dist, vd_narrow_band);
    
    vd_narrow_band.write(path_output + "/vd_narrow_band_images", FORMAT_BINARY); // Save particles as vtk file
    
    openfpm_finalize(); // Finalize openFPM library
    return 0;
}