|
OpenFPM_pdata
4.1.0
Project that contain the implementation of distributed structures
|
|
|
OpenFPM_pdata
4.1.0
Project that contain the implementation of distributed structures
|
|
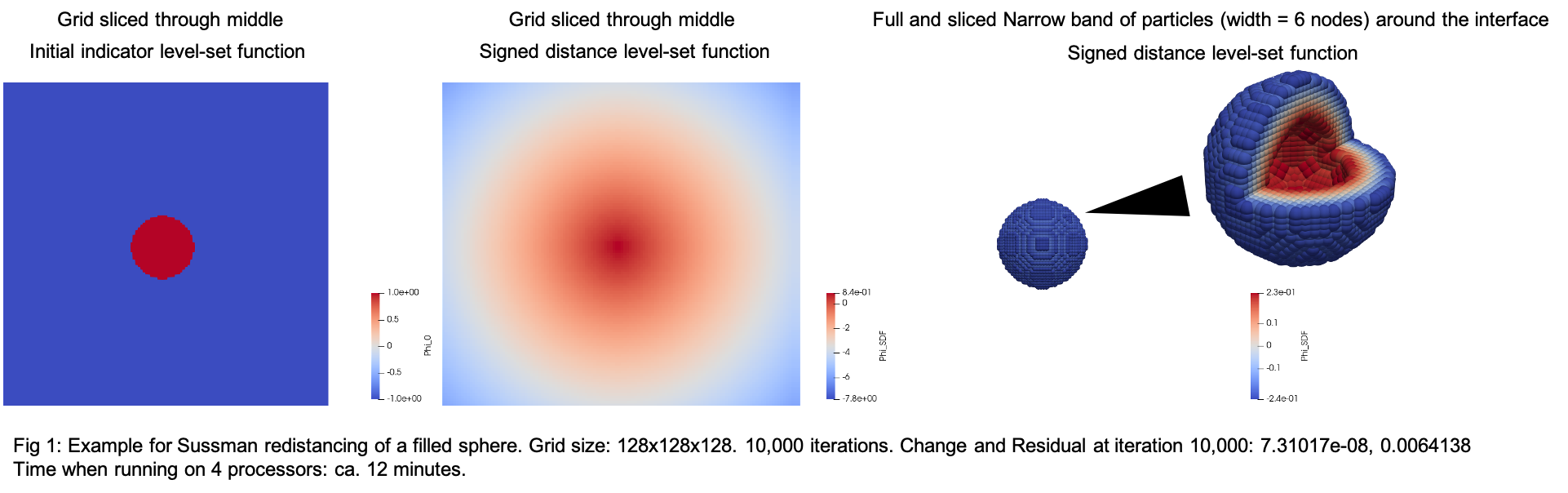
In this example, we perform Sussman redistancing on a filled 3D sphere. Here, the sphere is constructed via equation. For image based reconstruction and redistancing see Images 3D.
A filled sphere with center a, b, c can be constructed by the following equation:
\[ (x-a)^2 + (y-b)^2 + (z-c)^2 <= r^2 \]
We will create a filled sphere on a 3D grid, where the sphere is represented by a -1/+1 step function (indicator function) as:
\[ \phi_{\text{indicator}} = \begin{cases} +1 & \text{point lies inside the object} \\ 0 & \text{object surface} \\ -1 & \text{point lies outside the object} \\ \end{cases} \]
By Sussman redistancing, this indicator function is transformed into a signed distance function:
\[ \phi_{\text{SDF}} = \begin{cases} +d & \text{orthogonal distance to the closest surface of a point lying inside the object} \\ 0 & \text{object surface} \\ -d & \text{orthogonal distance to the closest surface of a point lying outside the object} \\ \end{cases} \]
Once we have received the Phi_SDF from the redistancing, particles can be placed on narrow band around the interface.
Output: print on promt : Iteration, Change, Residual (see: DistFromSol::change, DistFromSol::residual) writes vtk and hdf5 files of: 1.) 3D grid with sphere pre-redistancing and post-redistancing (Phi_0 and Phi_SDF, respectively) 2.) particles on narrow band around interface
These are the header files that we need to include:
We start with
Optionally, we can define the grid dimensionality and some indices for better code readability later on.
x: First dimensiony: Second dimensionz: Third dimensionPhi_0_grid: Index of property that stores the initial level-set-functionPhi_SDF_grid: Index of property where the redistancing result should be written to In order to get a grid, we
On the grid that we have just created, we can now initialize Phi_0 as a filled sphere of defined radius. The center of the sphere is passed as x_center and y_center (see Sphere.hpp). Phi_0 will then be:
\[ \phi_{\text{indicator}} = \begin{cases} +1 & \text{point lies inside the object} \\ 0 & \text{object surface} \\ -1 & \text{point lies outside the object} \\ \end{cases} \]
Optionally, we can save this initial grid as a vtk file, if we want to visualize and check it in Paraview.
For the redistancing, we can choose some options. These options will then be passed bundled as a structure to
the redistancing function. Setting these options is optional, since they all have a Default value as well. In particular the following options can be set by the user:
min_iter: Minimum number of iterations before steady state in narrow band will be checked (Default: 1e5).max_iter: Maximum number of iterations you want to run the redistancing, even if steady state might not yet have been reached (Default: 1e12).convTolChange.value: Convergence tolerance for the maximal change of Phi within the narrow band between two consecutive iterations (Default: 1e-15).convTolChange.check: Set true, if you want to use the maximal change of Phi between two iterations as measure of how close you are to the steady state solution. Redistancing will then stop if convTolChange.value is reached or if the current iteration is bigger than max_iter.convTolResidual.value: Convergence tolerance for the residual, that is max{abs(magnitude gradient of phi - 1)} of Phi in the narrow band (Default 1e-3).convTolResidual.check: Set true, if you want to use the residual of the current iteration as measure of how close you are to the steady state solution. Redistancing will then stop if convTolResidual.value is reached or if the current iteration is bigger than max_iter.interval_check_convergence: Interval of iterations at which convergence to steady state is checked (Default: 100).width_NB_in_grid_points: Width of narrow band in number of grid points. Must be at least 4, in order to have at least 2 grid points on each side of the interface. Is automatically set to 4, if a value smaller than 4 is chosen (Default: 4).print_current_iterChangeResidual: If true, the number of the current iteration, the corresponding change w.r.t the previous iteration and the residual is printed (Default: false).print_steadyState_iter: If true, the number of the steady-state-iteration, the corresponding change w.r.t the previous iteration and the residual is printed (Default: false).save_temp_grid: If true, save the temporary grid as hdf5 that can be reloaded onto a grid (Default: false).Now, we can instantiate the Sussman-redistancing class using the redist_options we have just set (or use the defaults) and run the redistancing. If we are interested in the time-step that was automatically computed internally according to the CFL-condition, we can access it with RedistancingSussman::get_time_step(). If, for whatever reason, we wish to change this timestep, we can do that with RedistancingSussman::set_user_time_step (T dt). However, be careful when setting your own timestep: if chosen too large, the CFL-condition may be no longer fulfilled and the method can become unstable. For the #run_redistancing we need to provide two template parameters. These are the indices of the respective property that: 1.) contains the initial Phi, 2.) should contain the output of the redistancing. You can use the same index twice, if you want that your input will be overwritten by the output. This time, it makes sense, to save the output grid, since this is already our grid containing the signed distance function in Prop. 2. The vtk-file can be opened in Paraview. If we want, we can further save the result as hdf5 file that can be reloaded onto an openFPM grid.
Next, we want to place particles in a narrow band around the interface. For this, we need to create an empty vector in the same domain as our grid from before. We therefore re-use the box and ghost that we defined during grid creation. This time, we have to set the boundary conditions (see general OpenFPM vector_dist documentation for details.) We also have to choose now, how many properties our particle should store. Minimum is one, but you can have particles with arbitrary many properties, depending on what you want to use them for later on. Here, we exemplarily define 3 properties.
Before we fill the empty vector that we just created with particles, we define how thick the narrow band around the interface should be. This is independent of the redist_options.width_NB_in_grid_points that we chose before. However, it makes sense to use a width during redistancing which is at least as large as the width that we want to place the particles in. The reason is that convergence criteria were checked for that part of the grid only, which belonged to the narrow band.
Depending on the type of the variable which you define, the width can be either set in terms of number of grid points (size_t), physical width (phi_type) or extension of narrow band as physical width inside of object and outside the object (phi_type, phi_type).
Again, we can define some indices for better code readability. This is just an example, you may want to choose different names and have a different number of properties thus different number of indices.
Now, we finally fill the vector with particles placed in a narrow band around the interface. The first template parameter that we pass, must always be the index of the grid property that contains the Phi_SDF.
Then you can decide between the following options, what you want to copy from the grid to the particles:
narrowBand.get_narrow_band<Phi_SDF_grid, Phi_SDF_vd>(g_dist, vd_narrow_band);narrowBand .get_narrow_band<Phi_SDF_grid, Phi_SDF_vd, Phi_grad_vd>(g_dist, vd_narrow_band);narrowBand.get_narrow_band<Phi_SDF_grid, Phi_SDF_vd, Phi_grad_vd, Phi_magnOfGrad_vd>(g_dist,
vd_narrow_band);narrowBand.get_narrow_band_copy_specific_property<Phi_SDF_grid, Prop_index_grid, Prop_index_vector>(g_dist, vd_narrow_band);We save the particles in a vtk file (open in Paraview) and as hdf5 file (can be loaded back on particles).
We end with terminating OpenFPM
1.9.8