OpenFPM_pdata  4.1.0
Project that contain the implementation of distributed structures
 
Loading...
Searching...
No Matches
Stokes Flow in a 3D Ball with Pressure Correction

Stokes incompressible 3D Ball

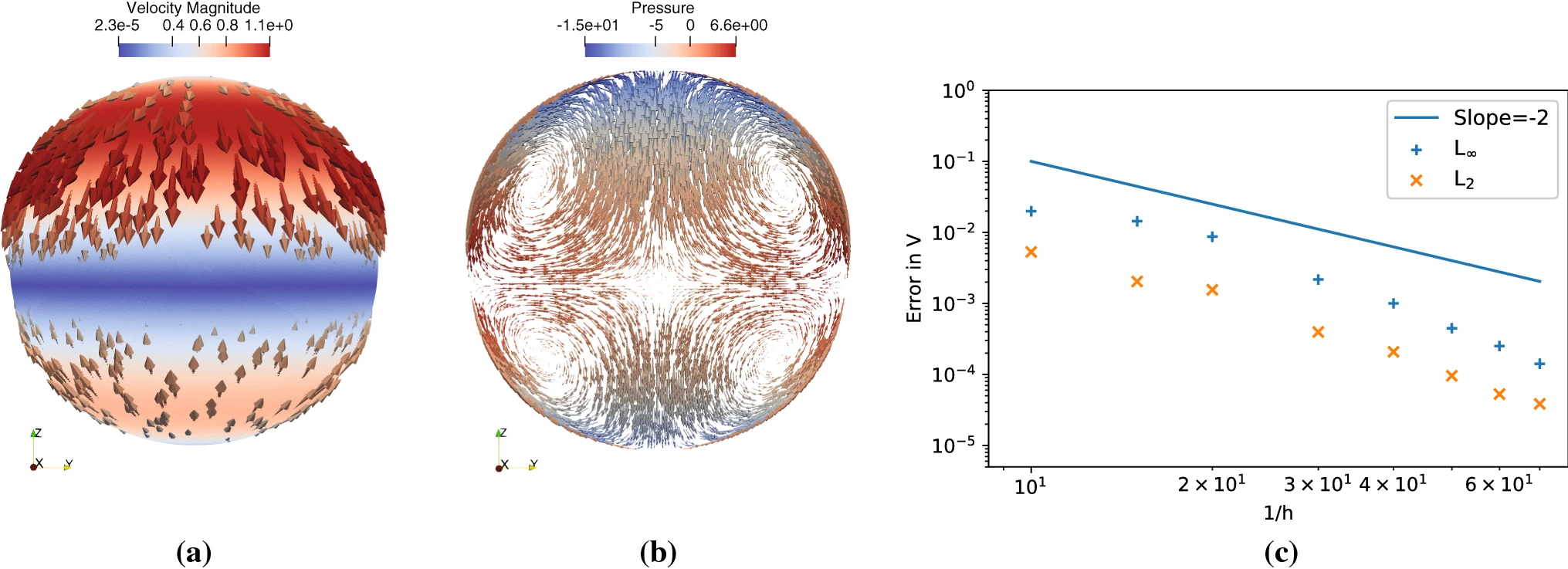
In this example, we solve the incompressible stokes equation in a 3D ball:

\[ \mathrm{\Delta} \mathbf{v} = \nabla \Pi\, , \qquad \mathbf{v}\in \Omega\backslash\partial\Omega \\ \nabla\cdot \mathbf{v}=0 \]

in 3d ball \(\Omega=\overline{B_1}(0)\subset \mathbb{R}^3\) with Dirichlet velocity boundary conditions as the analytical solution on the surface:

\[ \mathbf{v}=\sum\limits_{l=0}^{\infty}\sum\limits_{m=-l}^{l}u_{l m}^{r}(r) \mathbf{Y}^{(l m)}+u_{l m}^{(1)}(r) \mathbf{\Psi}^{(l m)}+u_{l m}^{(2)}(r) \mathbf{\Phi}^{(l m)}\\ \Pi=\sum_{l=0}^{\infty} \sum_{m=-l}^{l} p_{l m}(r) Y_{l m} \]

We do that by solving the implicit stokes equation and and employing an iterative pressure correction scheme:

Output: Stokes flow solution in a 3D Ball.

Including the headers

These are the header files that we need to include:

// Include Vector Expression,Vector Expressions for Subset,DCPSE , and Solver header files
#include "config.h"
#include <iostream>
#include "DCPSE/DCPSE_OP/DCPSE_op.hpp"
#include "DCPSE/DCPSE_OP/DCPSE_Solver.hpp"
#include "Operators/Vector/vector_dist_operators.hpp"
#include "Vector/vector_dist_subset.hpp"
#include "util/SphericalHarmonics.hpp"

Initialization

  • Initialize the library
  • Define some useful constants
  • define Ghost size
  • Non-periodic boundary conditions
openfpm_init(&argc,&argv);
timer tt2;
tt2.start();
size_t grd_sz = 18;
double V_err_eps = 5e-4;
double nu=1.0;
const size_t sz[3] = {grd_sz,grd_sz,grd_sz};
Box<3, double> box({-1.0, -1.0,-1.0}, {1.0,1.0,1.0});
size_t bc[3] = {NON_PERIODIC, NON_PERIODIC, NON_PERIODIC};
double spacing = 2.0 / (sz[0] - 1);
double rCut = 3.9*spacing;
double R=1.0;
Ghost<3, double> ghost(rCut);
// P V v_B RHS V_t P_anal RHS2 Polar cord
vector_dist_ws<3, double, aggregate<double,VectorS<3, double>,VectorS<3, double>,double,VectorS<3, double>,double,double,VectorS<3, double>,VectorS<3, double>,VectorS<3, double>>> Particles(0, box, bc, ghost);
Particles.setPropNames({"Pressure","Velocity","Velocity_Boundary","Divergence","V_T","P_analytical","TEMP" ,"RHS","PolarCoord","V_analytical"});
Box
This class represent an N-dimensional box.
Definition Box.hpp:61
Point
This class implement the point shape in an N-dimensional space.
Definition Point.hpp:28
timer
Class for cpu time benchmarking.
Definition timer.hpp:28
timer::start
void start()
Start the timer.
Definition timer.hpp:90
vector_dist_ws
Definition vector_dist_subset.hpp:17

Creating particles in the 3D ball and on the surface

auto &v_cl = create_vcluster();
auto it = Particles.getGridIterator(sz);
while (it.isNext()) {
auto key = it.get();
double x = -1.0+key.get(0) * it.getSpacing(0);
double y = -1.0+key.get(1) * it.getSpacing(1);
double z = -1.0+key.get(2) * it.getSpacing(2);
double r=sqrt(x*x+y*y+z*z);
if (r<R-spacing/2.0) {
Particles.add();
Particles.getLastPos()[0] = x;
Particles.getLastPos()[1] = y;
Particles.getLastPos()[2] = z;
Particles.getLastProp<8>()[0] = r;
if (r==0){
Particles.getLastProp<8>()[1] = 0.0;
}
else{
Particles.getLastProp<8>()[1] = std::atan2(sqrt(x*x+y*y),z);
}
Particles.getLastProp<8>()[2] = std::atan2(y,x);
}
++it;
}
int n_sp=int(grd_sz)*int(grd_sz)*3;
double Golden_angle=M_PI * (3.0 - sqrt(5.0));
for(int i=1;i<=n_sp;i++)
{
double y = 1.0 - (i /double(n_sp - 1.0)) * 2.0;
double radius = sqrt(1 - y * y);
double Golden_theta = Golden_angle * i;
double x = cos(Golden_theta) * radius;
double z = sin(Golden_theta) * radius;
if (acos(z)==0 || acos(z)==M_PI){
std::cout<<"Theta 0/Pi "<<std::endl;
continue;
}
Particles.add();
Particles.getLastPos()[0] = x;
Particles.getLastPos()[1] = y;
Particles.getLastPos()[2] = z;
Particles.getLastProp<8>()[0] = 1.0 ;
Particles.getLastProp<8>()[1] = std::atan2(sqrt(x*x+y*y),z);
Particles.getLastProp<8>()[2] = std::atan2(y,x);
}
Particles.map();
Particles.ghost_get<0>();
cub::int
KeyT const ValueT ValueT OffsetIteratorT OffsetIteratorT int
[in] The number of segments that comprise the sorting data
Definition dispatch_radix_sort.cuh:336

Encoding the analytical solution from vector spherical harmonics for comparison

std::unordered_map<const lm,double,key_hash,key_equal> Vr;
std::unordered_map<const lm,double,key_hash,key_equal> V1;
std::unordered_map<const lm,double,key_hash,key_equal> V2;
//Setting max mode l_max
constexpr int K = 2;
//Setting amplitudes to 0
for(int l=0;l<=K;l++){
for(int m=-l;m<=l;m++){
Vr[std::make_tuple(l,m)]=0.0;
V1[std::make_tuple(l,m)]=0.0;
V2[std::make_tuple(l,m)]=0.0;
}
}
//Setting some amplitude for boundary velocity
V1[std::make_tuple(2,0)]=1.0;
auto it2 = Particles.getDomainIterator();
while (it2.isNext()) {
auto p = it2.get();
Point<3, double> xp = Particles.getPos(p);
Point<3, double> xP = Particles.getProp<8>(p);
Particles.getProp<0>(p) =0;
if (xP[0]==1.0) {
Particles.getProp<0>(p) = 0;
std::vector<double> SVel;
SVel=openfpm::math::sumY<K>(xP[0],xP[1],xP[2],Vr,V1,V2);
double SP=openfpm::math::sumY_Scalar<K>(xP[0],xP[1],xP[2],Vr);
Particles.getProp<2>(p)[0] = SVel[0];
Particles.getProp<2>(p)[1] = SVel[1];
Particles.getProp<2>(p)[2] = SVel[2];
Particles.getProp<9>(p)[0] = SVel[0];
Particles.getProp<9>(p)[1] = SVel[1];
Particles.getProp<9>(p)[2] = SVel[2];
Particles.getProp<5>(p) = SP;
Particles.setSubset(p,1);
}
else {
Particles.setSubset(p,0);
Particles.getProp<0>(p) = 0;
Particles.getProp<1>(p)[0] = 0;
Particles.getProp<1>(p)[1] = 0;
Particles.getProp<1>(p)[2] = 0;
}
++it2;
}

Creating Bulk and Boundary partitions of the domain for imposing the boundary condition and equations

vector_dist_subset<3, double, aggregate<double,VectorS<3, double>,VectorS<3, double>,double,VectorS<3, double>,double,double,VectorS<3, double>,VectorS<3, double>,VectorS<3, double>>> Particles_bulk(Particles,0);
vector_dist_subset<3, double, aggregate<double,VectorS<3, double>,VectorS<3, double>,double,VectorS<3, double>,double,double,VectorS<3, double>,VectorS<3, double>,VectorS<3, double>>> Particles_surface(Particles,1);
auto & bulk = Particles_bulk.getIds();
auto & Surface = Particles_surface.getIds();
for (int j = 0; j < bulk.size(); j++) {
auto p = bulk.get<0>(j);
Point<3, double> xp = Particles.getPos(p);
Point<3, double> xP = Particles.getProp<8>(p);
//Dictionary for basis coefficients
std::unordered_map<const lm,double,key_hash,key_equal> Ur, U1, U2, Plm;
//Setting basis coefficients
for (int l = 0; l <= K; l++) {
for (int m = -l; m <= l; m++) {
auto Er= Vr.find(std::make_tuple(l,m));
auto E1= V1.find(std::make_tuple(l,m));
auto E2= V2.find(std::make_tuple(l,m));
std::vector<double> Sol=openfpm::math::sph_anasol_u(nu,l,m,Er->second,E1->second,E2->second,xP[0]);
Ur[std::make_tuple(l,m)]=Sol[0];
U1[std::make_tuple(l,m)]=Sol[1];
U2[std::make_tuple(l,m)]=Sol[2];
Plm[std::make_tuple(l,m)]=Sol[3];
}
}
//Computing Analyical Solution.
if(fabs(xP[0])>=1e-5 && xP[1]>1e-5 && (M_PI-xP[1])>=1e-5)
{
std::vector<double> SVel = openfpm::math::sumY<K>(xP[0], xP[1], xP[2], Ur, U1, U2);
Particles.getProp<9>(p)[0] = SVel[0];
Particles.getProp<9>(p)[1] = SVel[1];
Particles.getProp<9>(p)[2] = SVel[2];
Particles.getProp<5>(p) = openfpm::math::sumY_Scalar<K>(xP[0], xP[1], xP[2], Plm);
}
}
vector_dist_subset
Definition vector_dist_subset.hpp:84

Creating a 3D implicit solver for the given set of particles and iteratively solving wit pressure correction.

auto P = getV<0>(Particles);
auto V = getV<1>(Particles);
auto V_B = getV<2>(Particles);
V.setVarId(0);
auto DIV = getV<3>(Particles);
auto V_t = getV<4>(Particles);
auto P_anal = getV<5>(Particles);
auto temp=getV<6>(Particles);
auto RHS = getV<7>(Particles);
auto P_bulk = getV<0>(Particles_bulk);
auto RHS_bulk = getV<7>(Particles_bulk);
auto V_anal = getV<9>(Particles);
V_t=V;
P=0;
P_bulk=0;
double sampling=3.1;
double sampling2=1.9;
double rCut2=3.9*spacing;
Derivative_x Dx(Particles, 2, rCut,sampling, support_options::RADIUS),B_Dx(Particles_bulk, 2, rCut,sampling, support_options::RADIUS);
Derivative_y Dy(Particles, 2, rCut,sampling, support_options::RADIUS),B_Dy(Particles_bulk, 2, rCut,sampling, support_options::RADIUS);
Derivative_z Dz(Particles, 2, rCut,sampling, support_options::RADIUS),B_Dz(Particles_bulk, 2, rCut,sampling, support_options::RADIUS);
Derivative_xx Dxx(Particles, 2, rCut2,sampling2,support_options::RADIUS);
Derivative_yy Dyy(Particles, 2, rCut2,sampling2,support_options::RADIUS);
Derivative_zz Dzz(Particles, 2, rCut2,sampling2,support_options::RADIUS);
Point_test
Test structure used for several test.
Definition Point_test.hpp:106

Creating a 3D implicit solver for the given set of particles and iterativelt solving wit pressure correction. ## {#3dballsol}

eq_id vx,vy,vz;
vx.setId(0);
vy.setId(1);
vz.setId(2);
petsc_solver<double> solverPetsc;
solverPetsc.setPreconditioner(PCNONE);
timer tt;
double sum=0,sum1=0;
V_t=V;
double V_err = 1, V_err_old;
int n = 0, nmax = 30, ctr = 0, errctr, Vreset = 0;
V_err = 1;
n = 0;
tt.start();
while (V_err >= V_err_eps && n <= nmax) {
Particles.ghost_get<0>(SKIP_LABELLING);
RHS_bulk[0] = B_Dx(P);
RHS_bulk[1] = B_Dy(P);
RHS_bulk[2] = B_Dz(P);
DCPSE_scheme<equations3d3, decltype(Particles)> Solver(Particles);
auto Stokes1 = nu * (Dxx(V[0])+Dyy(V[0])+Dzz(V[0]));
auto Stokes2 = nu * (Dxx(V[1])+Dyy(V[1])+Dzz(V[1]));
auto Stokes3 = nu * (Dxx(V[2])+Dyy(V[2])+Dzz(V[2]));
Solver.impose(Stokes1, bulk, RHS[0], vx);
Solver.impose(Stokes2, bulk, RHS[1], vy);
Solver.impose(Stokes3, bulk, RHS[2], vz);
Solver.impose(V[0], Surface, V_B[0], vx);
Solver.impose(V[1], Surface, V_B[1], vy);
Solver.impose(V[2], Surface, V_B[2], vz);
Solver.solve_with_solver(solverPetsc, V[0], V[1], V[2]);
Particles.ghost_get<1>();
DIV = -(Dx(V[0])+Dy(V[1])+Dz(V[2]));
P_bulk = P + DIV;
sum = 0;
sum1 = 0;
for (int j = 0; j < bulk.size(); j++) {
auto p = bulk.get<0>(j);
sum += (Particles.getProp<4>(p)[0] - Particles.getProp<1>(p)[0]) *
(Particles.getProp<4>(p)[0] - Particles.getProp<1>(p)[0]) +
(Particles.getProp<4>(p)[1] - Particles.getProp<1>(p)[1]) *
(Particles.getProp<4>(p)[1] - Particles.getProp<1>(p)[1]) +
(Particles.getProp<4>(p)[2] - Particles.getProp<1>(p)[2]) *
(Particles.getProp<4>(p)[2] - Particles.getProp<1>(p)[2]);
sum1 += Particles.getProp<1>(p)[0] * Particles.getProp<1>(p)[0] +
Particles.getProp<1>(p)[1] * Particles.getProp<1>(p)[1] +
Particles.getProp<1>(p)[2] * Particles.getProp<1>(p)[2];
}
sum = sqrt(sum);
sum1 = sqrt(sum1);
v_cl.sum(sum);
v_cl.sum(sum1);
v_cl.execute();
V_t = V;
Particles.ghost_get<1>(SKIP_LABELLING);
V_err_old = V_err;
V_err = sum / sum1;
if (V_err > V_err_old || abs(V_err_old - V_err) < 1e-14) {
errctr++;
} else {
errctr = 0;
}
if (n > 3) {
if (errctr > 1) {
std::cout << "CONVERGENCE LOOP BROKEN DUE TO INCREASE/VERY SLOW DECREASE IN Divergence" << std::endl;
Vreset = 1;
break;
} else {
Vreset = 0;
}
}
n++;
}
//Writing the final Solution
//The solution can be visualized at https://link.springer.com/article/10.1140/epje/s10189-021-00121-x/figures/7
Particles.write("StokesSphere");
} //Ending Scope for Petsc.
//Finalizing the Library.
openfpm_finalize();
eq_id
Definition eq_solve_common.hpp:15
petsc_solver
In case T does not match the PETSC precision compilation create a stub structure.
Definition petsc_solver.hpp:56
sum
It model an expression expr1 + ... exprn.
Definition sum.hpp:93

Full code

//
// Created by Abhinav Singh on 15.06.20.
//
// Include Vector Expression,Vector Expressions for Subset,DCPSE , and Solver header files
#include "config.h"
#include <iostream>
#include "DCPSE/DCPSE_OP/DCPSE_op.hpp"
#include "DCPSE/DCPSE_OP/DCPSE_Solver.hpp"
#include "Operators/Vector/vector_dist_operators.hpp"
#include "Vector/vector_dist_subset.hpp"
#include "util/SphericalHarmonics.hpp"
int main(int argc, char* argv[])
{
{
openfpm_init(&argc,&argv);
timer tt2;
tt2.start();
size_t grd_sz = 18;
double V_err_eps = 5e-4;
double nu=1.0;
const size_t sz[3] = {grd_sz,grd_sz,grd_sz};
Box<3, double> box({-1.0, -1.0,-1.0}, {1.0,1.0,1.0});
size_t bc[3] = {NON_PERIODIC, NON_PERIODIC, NON_PERIODIC};
double spacing = 2.0 / (sz[0] - 1);
double rCut = 3.9*spacing;
double R=1.0;
Ghost<3, double> ghost(rCut);
// P V v_B RHS V_t P_anal RHS2 Polar cord
vector_dist_ws<3, double, aggregate<double,VectorS<3, double>,VectorS<3, double>,double,VectorS<3, double>,double,double,VectorS<3, double>,VectorS<3, double>,VectorS<3, double>>> Particles(0, box, bc, ghost);
Particles.setPropNames({"Pressure","Velocity","Velocity_Boundary","Divergence","V_T","P_analytical","TEMP" ,"RHS","PolarCoord","V_analytical"});
auto &v_cl = create_vcluster();
auto it = Particles.getGridIterator(sz);
while (it.isNext()) {
auto key = it.get();
double x = -1.0+key.get(0) * it.getSpacing(0);
double y = -1.0+key.get(1) * it.getSpacing(1);
double z = -1.0+key.get(2) * it.getSpacing(2);
double r=sqrt(x*x+y*y+z*z);
if (r<R-spacing/2.0) {
Particles.add();
Particles.getLastPos()[0] = x;
Particles.getLastPos()[1] = y;
Particles.getLastPos()[2] = z;
Particles.getLastProp<8>()[0] = r;
if (r==0){
Particles.getLastProp<8>()[1] = 0.0;
}
else{
Particles.getLastProp<8>()[1] = std::atan2(sqrt(x*x+y*y),z);
}
Particles.getLastProp<8>()[2] = std::atan2(y,x);
}
++it;
}
int n_sp=int(grd_sz)*int(grd_sz)*3;
double Golden_angle=M_PI * (3.0 - sqrt(5.0));
for(int i=1;i<=n_sp;i++)
{
double y = 1.0 - (i /double(n_sp - 1.0)) * 2.0;
double radius = sqrt(1 - y * y);
double Golden_theta = Golden_angle * i;
double x = cos(Golden_theta) * radius;
double z = sin(Golden_theta) * radius;
if (acos(z)==0 || acos(z)==M_PI){
std::cout<<"Theta 0/Pi "<<std::endl;
continue;
}
Particles.add();
Particles.getLastPos()[0] = x;
Particles.getLastPos()[1] = y;
Particles.getLastPos()[2] = z;
Particles.getLastProp<8>()[0] = 1.0 ;
Particles.getLastProp<8>()[1] = std::atan2(sqrt(x*x+y*y),z);
Particles.getLastProp<8>()[2] = std::atan2(y,x);
}
Particles.map();
Particles.ghost_get<0>();
std::unordered_map<const lm,double,key_hash,key_equal> Vr;
std::unordered_map<const lm,double,key_hash,key_equal> V1;
std::unordered_map<const lm,double,key_hash,key_equal> V2;
//Setting max mode l_max
constexpr int K = 2;
//Setting amplitudes to 0
for(int l=0;l<=K;l++){
for(int m=-l;m<=l;m++){
Vr[std::make_tuple(l,m)]=0.0;
V1[std::make_tuple(l,m)]=0.0;
V2[std::make_tuple(l,m)]=0.0;
}
}
//Setting some amplitude for boundary velocity
V1[std::make_tuple(2,0)]=1.0;
auto it2 = Particles.getDomainIterator();
while (it2.isNext()) {
auto p = it2.get();
Point<3, double> xp = Particles.getPos(p);
Point<3, double> xP = Particles.getProp<8>(p);
Particles.getProp<0>(p) =0;
if (xP[0]==1.0) {
Particles.getProp<0>(p) = 0;
std::vector<double> SVel;
SVel=openfpm::math::sumY<K>(xP[0],xP[1],xP[2],Vr,V1,V2);
double SP=openfpm::math::sumY_Scalar<K>(xP[0],xP[1],xP[2],Vr);
Particles.getProp<2>(p)[0] = SVel[0];
Particles.getProp<2>(p)[1] = SVel[1];
Particles.getProp<2>(p)[2] = SVel[2];
Particles.getProp<9>(p)[0] = SVel[0];
Particles.getProp<9>(p)[1] = SVel[1];
Particles.getProp<9>(p)[2] = SVel[2];
Particles.getProp<5>(p) = SP;
Particles.setSubset(p,1);
}
else {
Particles.setSubset(p,0);
Particles.getProp<0>(p) = 0;
Particles.getProp<1>(p)[0] = 0;
Particles.getProp<1>(p)[1] = 0;
Particles.getProp<1>(p)[2] = 0;
}
++it2;
}
vector_dist_subset<3, double, aggregate<double,VectorS<3, double>,VectorS<3, double>,double,VectorS<3, double>,double,double,VectorS<3, double>,VectorS<3, double>,VectorS<3, double>>> Particles_bulk(Particles,0);
vector_dist_subset<3, double, aggregate<double,VectorS<3, double>,VectorS<3, double>,double,VectorS<3, double>,double,double,VectorS<3, double>,VectorS<3, double>,VectorS<3, double>>> Particles_surface(Particles,1);
auto & bulk = Particles_bulk.getIds();
auto & Surface = Particles_surface.getIds();
for (int j = 0; j < bulk.size(); j++) {
auto p = bulk.get<0>(j);
Point<3, double> xp = Particles.getPos(p);
Point<3, double> xP = Particles.getProp<8>(p);
//Dictionary for basis coefficients
std::unordered_map<const lm,double,key_hash,key_equal> Ur, U1, U2, Plm;
//Setting basis coefficients
for (int l = 0; l <= K; l++) {
for (int m = -l; m <= l; m++) {
auto Er= Vr.find(std::make_tuple(l,m));
auto E1= V1.find(std::make_tuple(l,m));
auto E2= V2.find(std::make_tuple(l,m));
std::vector<double> Sol=openfpm::math::sph_anasol_u(nu,l,m,Er->second,E1->second,E2->second,xP[0]);
Ur[std::make_tuple(l,m)]=Sol[0];
U1[std::make_tuple(l,m)]=Sol[1];
U2[std::make_tuple(l,m)]=Sol[2];
Plm[std::make_tuple(l,m)]=Sol[3];
}
}
//Computing Analyical Solution.
if(fabs(xP[0])>=1e-5 && xP[1]>1e-5 && (M_PI-xP[1])>=1e-5)
{
std::vector<double> SVel = openfpm::math::sumY<K>(xP[0], xP[1], xP[2], Ur, U1, U2);
Particles.getProp<9>(p)[0] = SVel[0];
Particles.getProp<9>(p)[1] = SVel[1];
Particles.getProp<9>(p)[2] = SVel[2];
Particles.getProp<5>(p) = openfpm::math::sumY_Scalar<K>(xP[0], xP[1], xP[2], Plm);
}
}
auto P = getV<0>(Particles);
auto V = getV<1>(Particles);
auto V_B = getV<2>(Particles);
V.setVarId(0);
auto DIV = getV<3>(Particles);
auto V_t = getV<4>(Particles);
auto P_anal = getV<5>(Particles);
auto temp=getV<6>(Particles);
auto RHS = getV<7>(Particles);
auto P_bulk = getV<0>(Particles_bulk);
auto RHS_bulk = getV<7>(Particles_bulk);
auto V_anal = getV<9>(Particles);
V_t=V;
P=0;
P_bulk=0;
double sampling=3.1;
double sampling2=1.9;
double rCut2=3.9*spacing;
Derivative_x Dx(Particles, 2, rCut,sampling, support_options::RADIUS),B_Dx(Particles_bulk, 2, rCut,sampling, support_options::RADIUS);
Derivative_y Dy(Particles, 2, rCut,sampling, support_options::RADIUS),B_Dy(Particles_bulk, 2, rCut,sampling, support_options::RADIUS);
Derivative_z Dz(Particles, 2, rCut,sampling, support_options::RADIUS),B_Dz(Particles_bulk, 2, rCut,sampling, support_options::RADIUS);
Derivative_xx Dxx(Particles, 2, rCut2,sampling2,support_options::RADIUS);
Derivative_yy Dyy(Particles, 2, rCut2,sampling2,support_options::RADIUS);
Derivative_zz Dzz(Particles, 2, rCut2,sampling2,support_options::RADIUS);
eq_id vx,vy,vz;
vx.setId(0);
vy.setId(1);
vz.setId(2);
petsc_solver<double> solverPetsc;
solverPetsc.setPreconditioner(PCNONE);
timer tt;
double sum=0,sum1=0;
V_t=V;
double V_err = 1, V_err_old;
int n = 0, nmax = 30, ctr = 0, errctr, Vreset = 0;
V_err = 1;
n = 0;
tt.start();
while (V_err >= V_err_eps && n <= nmax) {
Particles.ghost_get<0>(SKIP_LABELLING);
RHS_bulk[0] = B_Dx(P);
RHS_bulk[1] = B_Dy(P);
RHS_bulk[2] = B_Dz(P);
DCPSE_scheme<equations3d3, decltype(Particles)> Solver(Particles);
auto Stokes1 = nu * (Dxx(V[0])+Dyy(V[0])+Dzz(V[0]));
auto Stokes2 = nu * (Dxx(V[1])+Dyy(V[1])+Dzz(V[1]));
auto Stokes3 = nu * (Dxx(V[2])+Dyy(V[2])+Dzz(V[2]));
Solver.impose(Stokes1, bulk, RHS[0], vx);
Solver.impose(Stokes2, bulk, RHS[1], vy);
Solver.impose(Stokes3, bulk, RHS[2], vz);
Solver.impose(V[0], Surface, V_B[0], vx);
Solver.impose(V[1], Surface, V_B[1], vy);
Solver.impose(V[2], Surface, V_B[2], vz);
Solver.solve_with_solver(solverPetsc, V[0], V[1], V[2]);
Particles.ghost_get<1>();
DIV = -(Dx(V[0])+Dy(V[1])+Dz(V[2]));
P_bulk = P + DIV;
sum = 0;
sum1 = 0;
for (int j = 0; j < bulk.size(); j++) {
auto p = bulk.get<0>(j);
sum += (Particles.getProp<4>(p)[0] - Particles.getProp<1>(p)[0]) *
(Particles.getProp<4>(p)[0] - Particles.getProp<1>(p)[0]) +
(Particles.getProp<4>(p)[1] - Particles.getProp<1>(p)[1]) *
(Particles.getProp<4>(p)[1] - Particles.getProp<1>(p)[1]) +
(Particles.getProp<4>(p)[2] - Particles.getProp<1>(p)[2]) *
(Particles.getProp<4>(p)[2] - Particles.getProp<1>(p)[2]);
sum1 += Particles.getProp<1>(p)[0] * Particles.getProp<1>(p)[0] +
Particles.getProp<1>(p)[1] * Particles.getProp<1>(p)[1] +
Particles.getProp<1>(p)[2] * Particles.getProp<1>(p)[2];
}
sum = sqrt(sum);
sum1 = sqrt(sum1);
v_cl.sum(sum);
v_cl.sum(sum1);
v_cl.execute();
V_t = V;
Particles.ghost_get<1>(SKIP_LABELLING);
V_err_old = V_err;
V_err = sum / sum1;
if (V_err > V_err_old || abs(V_err_old - V_err) < 1e-14) {
errctr++;
} else {
errctr = 0;
}
if (n > 3) {
if (errctr > 1) {
std::cout << "CONVERGENCE LOOP BROKEN DUE TO INCREASE/VERY SLOW DECREASE IN Divergence" << std::endl;
Vreset = 1;
break;
} else {
Vreset = 0;
}
}
n++;
}
//Writing the final Solution
//The solution can be visualized at https://link.springer.com/article/10.1140/epje/s10189-021-00121-x/figures/7
Particles.write("StokesSphere");
} //Ending Scope for Petsc.
//Finalizing the Library.
openfpm_finalize();
}