Simple example of grid usage to solve an equation

This example show the usage of grid to solve the following equation

\(\frac{\partial^2 u}{\partial^2 x} + \frac{\partial^2 u}{\partial^2 y} = 1\)

\(u(x,y) = 0 \)

at the boundary. This lead to the solution shown in the picture

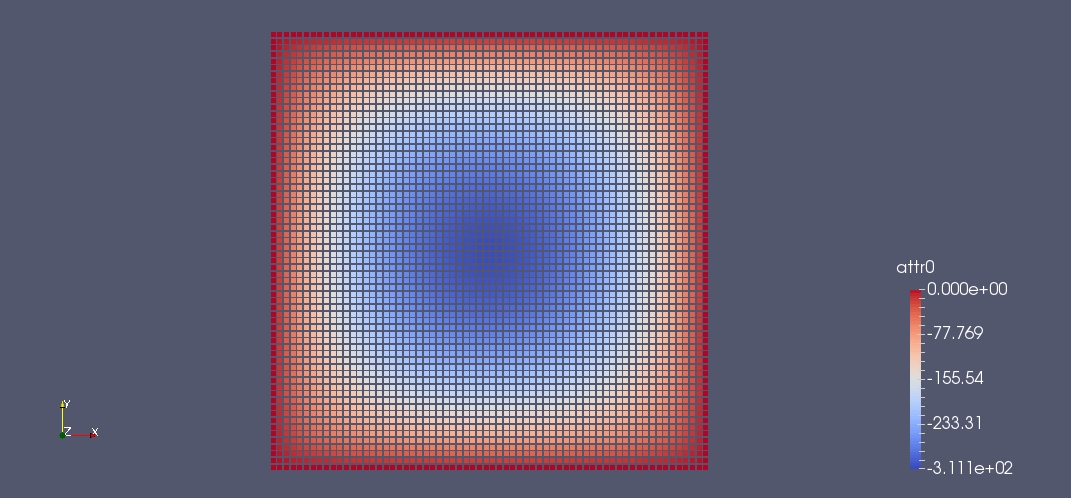
Field initialization

In order to initialize the field U, first we get an iterator that cover domain + Ghost to iterate all the grid points. Inside the cycle we initialize domain and border (Ghost part to 0.0)

See also: Loop over grid points

Get the local grid key

See also: Grid coordinates

 
        auto key = it.get();
 

Here we convert the local grid position, into global position. key_g contain 3 integers that identify the position of the grid point in global coordinates

See also: Grid coordinates

 
        auto key_g = g_dist.getGKey(key);
 

Initialize to 0, domain + boundary (Careful the end of the domain is at the point -1 and the point sz, where sz is the grid size in that dimension )

 
        if (key_g.get(0) < 0 || key_g.get(0) == sz[0] ||
            key_g.get(1) < 0 || key_g.get(1) == sz[1])
        {
            // Boundary part
            g_dist.template get<0>(key) = 0.0;
        }
        else
        {
            // Internal part
            g_dist.template get<0>(key) = 0.0;
        }
 

The full function look like this

 
void init(grid_dist_id<2,double,aggregate<double> > & g_dist, const size_t (& sz)[2])
{
 
    // Get the iterator
    auto it = g_dist.getDomainGhostIterator();
 
    // For each point in the grid
    while (it.isNext())
    {
 
        auto key = it.get();
 
        auto key_g = g_dist.getGKey(key);
 
        if (key_g.get(0) < 0 || key_g.get(0) == sz[0] ||
            key_g.get(1) < 0 || key_g.get(1) == sz[1])
        {
            // Boundary part
            g_dist.template get<0>(key) = 0.0;
        }
        else
        {
            // Internal part
            g_dist.template get<0>(key) = 0.0;
        }
 
        ++it;
 
    }
 
}

Initialization

Initialize the library

See also: Initialization

 
    openfpm_init(&argc,&argv);
    

Grid instantiation and initialization

Create

A 2D box that define the domain
an array of 2 unsigned integer that will define the size of the grid on each dimension
A Ghost object that will define the extension of the ghost part for each sub-domain in grid point unit

 
    Box<2,double> domain({-1.0,-1.0},{1.0,1.0});
    size_t sz[2] = {64,64};
    
    periodicity<2> bc = {NON_PERIODIC,NON_PERIODIC};
    
    // Ghost in grid unit
    Ghost<2,long int> g(1);

Create a distributed grid in 2D (1° template parameter) space in with double precision (2° template parameter) each grid point contain a scalar (double),

Constructor parameters:

sz: size of the grid on each dimension
domain: where the grid is defined
g: ghost extension
bc: boundary conditions

See also: Grid instantiation

 
    grid_dist_id<2, double, aggregate<double>> g_dist(sz,domain,g,bc);
    
    // spacing between two points
    double spacing[2] = {g_dist.spacing(0),g_dist.spacing(1)};

Initialize U and fill the boundary conditions

See also: e2_se_field_init

 
    init(g_dist,sz);
 

%Ghost synchronization

Before the computation read the ghost point we have to guarantee that they have updated values.

 
    // sync the ghost property 0
    g_dist.template ghost_get<0>();

Red-Black alghorithm

Do 10000 iteration of Red-Black Gauss-Siedel iterations

Get an iterator that go through the points of the grid (No ghost) To compute one iteration.

See also: Loop over grid points; Grid coordinates

 
        auto dom = g_dist.getDomainIterator();
        
        // Iterate over all the points
        while (dom.isNext())
        {
 
            // Get the local grid key
            auto key = dom.get();
 
            // Here we convert the local grid position, into global position, key_g contain 3 integers that identify the position
            // of the grid point in global coordinates
            auto key_g = g_dist.getGKey(key);
 
 
            //
            // If we are processing red and is odd jump to the next point
            // If we are processing black and is even jump to the next point
            //
            if (red_black == false && (key_g.get(0) + key_g.get(1)) % 2 == 0)
            {++dom; continue;}
            else if (red_black == true && (key_g.get(0) + key_g.get(1)) % 2 == 1)
            {++dom; continue;}
 
            //
            // Update the grid values
            //
            // P.S. The keyword template is removed, it is possible only if we are in a function
            // without template parameters (if you are unsure use the keyword template)
            //
            g_dist.get<0>(key) = (g_dist.get<0>(key.move(x,1)) + g_dist.template get<0>(key.move(x,-1)) +
                                 g_dist.get<0>(key.move(y,1)) + g_dist.template get<0>(key.move(y,-1)) +
                                 - 1.0)/4.0;
 
            //
            // next point (red/black)
            ++dom;
        }
 

Once an iteration is done we have to synchronize the ghosts to start a new iteration. Consider that we calculated the red points in the next iteration the red points in the ghost are used in reading. This mean that the ghost must have the updated values

 
        g_dist.template ghost_get<0>();
 
        // switch from red to black or black to red
        red_black = !red_black;

The full Algorithm look like this

 
    // flag that indicate if we are processing red or black
    // we start from red
    bool red_black = true;
 
    // 10000 iterations
    for (size_t i = 0 ; i < 10000 ; i++)
    {
 
        auto dom = g_dist.getDomainIterator();
        
        // Iterate over all the points
        while (dom.isNext())
        {
 
            // Get the local grid key
            auto key = dom.get();
 
            // Here we convert the local grid position, into global position, key_g contain 3 integers that identify the position
            // of the grid point in global coordinates
            auto key_g = g_dist.getGKey(key);
 
 
            //
            // If we are processing red and is odd jump to the next point
            // If we are processing black and is even jump to the next point
            //
            if (red_black == false && (key_g.get(0) + key_g.get(1)) % 2 == 0)
            {++dom; continue;}
            else if (red_black == true && (key_g.get(0) + key_g.get(1)) % 2 == 1)
            {++dom; continue;}
 
            //
            // Update the grid values
            //
            // P.S. The keyword template is removed, it is possible only if we are in a function
            // without template parameters (if you are unsure use the keyword template)
            //
            g_dist.get<0>(key) = (g_dist.get<0>(key.move(x,1)) + g_dist.template get<0>(key.move(x,-1)) +
                                 g_dist.get<0>(key.move(y,1)) + g_dist.template get<0>(key.move(y,-1)) +
                                 - 1.0)/4.0;
 
            //
            // next point (red/black)
            ++dom;
        }
 
 
 
        g_dist.template ghost_get<0>();
 
        // switch from red to black or black to red
        red_black = !red_black;
 
    }
    

Solution statistic

Once we got the solution we want to check if it really satisfy the equation, and calculate the error (norm infinity)

 
    // It contain the error
    double error = 0.0;
 
    // Get the iterator
    auto dom = g_dist.getDomainIterator();
 
    // Iterate over all the points
    while (dom.isNext())
    {
        // same the the grid point and the global grid point
        auto key = dom.get();
 
        // Calculate the error on each point
        // The error is how much the solution does not respect the equation
        double error_tmp = abs((g_dist.get<0>(key.move(x,1)) + g_dist.get<0>(key.move(x,-1)) +
                           g_dist.get<0>(key.move(y,1)) + g_dist.get<0>(key.move(y,-1)) +
                           - 4.0*g_dist.get<0>(key)) - 1.0);
 
        // In the norm infinity the maximum error across all the point is
        // important
        if (error_tmp > error)
            error = error_tmp;
 
        // next point
        ++dom;
 
    }
 
    // Get the maximum across processor to calculate the norm infinity of the error
    // Norm infinity of the error is the maximum error across all the grid points
    Vcluster<> & v_cl = create_vcluster();
    v_cl.max(error);
    v_cl.execute();
 
    // Only master print the norm infinity
    if (v_cl.getProcessUnitID() == 0)
            std::cout << "Error norm infinity: " << error << std::endl;
 

VTK Write and visualization

Finally we want a nice output to visualize the information stored by the distributed grid. The function write by default produce VTK files. One for each processor that can be visualized with the programs like paraview

See also: VTK and visualization

 
    g_dist.write("output");
 

Finalize

At the very end of the program we have always to de-initialize the library

 
    openfpm_finalize();
 

Full code

#include "Grid/grid_dist_id.hpp"
#include "data_type/aggregate.hpp"
 
 
void init(grid_dist_id<2,double,aggregate<double> > & g_dist, const size_t (& sz)[2])
{
 
    // Get the iterator
    auto it = g_dist.getDomainGhostIterator();
 
    // For each point in the grid
    while (it.isNext())
    {
 
 
        auto key = it.get();
 
 
 
        auto key_g = g_dist.getGKey(key);
 
 
 
        if (key_g.get(0) < 0 || key_g.get(0) == sz[0] ||
            key_g.get(1) < 0 || key_g.get(1) == sz[1])
        {
            // Boundary part
            g_dist.template get<0>(key) = 0.0;
        }
        else
        {
            // Internal part
            g_dist.template get<0>(key) = 0.0;
        }
 
 
 
        ++it;
 
    }
 
}
 
 
constexpr int x = 0;
constexpr int y = 1;
 
int main(int argc, char* argv[])
{
 
    openfpm_init(&argc,&argv);
    
 
 
    Box<2,double> domain({-1.0,-1.0},{1.0,1.0});
    size_t sz[2] = {64,64};
    
    periodicity<2> bc = {NON_PERIODIC,NON_PERIODIC};
    
    // Ghost in grid unit
    Ghost<2,long int> g(1);
    
 
 
    grid_dist_id<2, double, aggregate<double>> g_dist(sz,domain,g,bc);
    
    // spacing between two points
    double spacing[2] = {g_dist.spacing(0),g_dist.spacing(1)};
 
 
 
    init(g_dist,sz);
 
 
 
    // sync the ghost property 0
    g_dist.template ghost_get<0>();
 
 
 
    // flag that indicate if we are processing red or black
    // we start from red
    bool red_black = true;
 
    // 10000 iterations
    for (size_t i = 0 ; i < 10000 ; i++)
    {
 
        auto dom = g_dist.getDomainIterator();
        
        // Iterate over all the points
        while (dom.isNext())
        {
 
            // Get the local grid key
            auto key = dom.get();
 
            // Here we convert the local grid position, into global position, key_g contain 3 integers that identify the position
            // of the grid point in global coordinates
            auto key_g = g_dist.getGKey(key);
 
 
            //
            // If we are processing red and is odd jump to the next point
            // If we are processing black and is even jump to the next point
            //
            if (red_black == false && (key_g.get(0) + key_g.get(1)) % 2 == 0)
            {++dom; continue;}
            else if (red_black == true && (key_g.get(0) + key_g.get(1)) % 2 == 1)
            {++dom; continue;}
 
            //
            // Update the grid values
            //
            // P.S. The keyword template is removed, it is possible only if we are in a function
            // without template parameters (if you are unsure use the keyword template)
            //
            g_dist.get<0>(key) = (g_dist.get<0>(key.move(x,1)) + g_dist.template get<0>(key.move(x,-1)) +
                                 g_dist.get<0>(key.move(y,1)) + g_dist.template get<0>(key.move(y,-1)) +
                                 - 1.0)/4.0;
 
            //
            // next point (red/black)
            ++dom;
        }
 
 
 
        g_dist.template ghost_get<0>();
 
        // switch from red to black or black to red
        red_black = !red_black;
 
    }
    
 
 
    // It contain the error
    double error = 0.0;
 
    // Get the iterator
    auto dom = g_dist.getDomainIterator();
 
    // Iterate over all the points
    while (dom.isNext())
    {
        // same the the grid point and the global grid point
        auto key = dom.get();
 
        // Calculate the error on each point
        // The error is how much the solution does not respect the equation
        double error_tmp = abs((g_dist.get<0>(key.move(x,1)) + g_dist.get<0>(key.move(x,-1)) +
                           g_dist.get<0>(key.move(y,1)) + g_dist.get<0>(key.move(y,-1)) +
                           - 4.0*g_dist.get<0>(key)) - 1.0);
 
        // In the norm infinity the maximum error across all the point is
        // important
        if (error_tmp > error)
            error = error_tmp;
 
        // next point
        ++dom;
 
    }
 
    // Get the maximum across processor to calculate the norm infinity of the error
    // Norm infinity of the error is the maximum error across all the grid points
    Vcluster<> & v_cl = create_vcluster();
    v_cl.max(error);
    v_cl.execute();
 
    // Only master print the norm infinity
    if (v_cl.getProcessUnitID() == 0)
            std::cout << "Error norm infinity: " << error << std::endl;
 
 
 
    g_dist.write("output");
 
    
 
 
    openfpm_finalize();
 
 
}