Vector 7 SPH Dam break simulation with Dynamic load balacing

SPH with Dynamic load Balancing

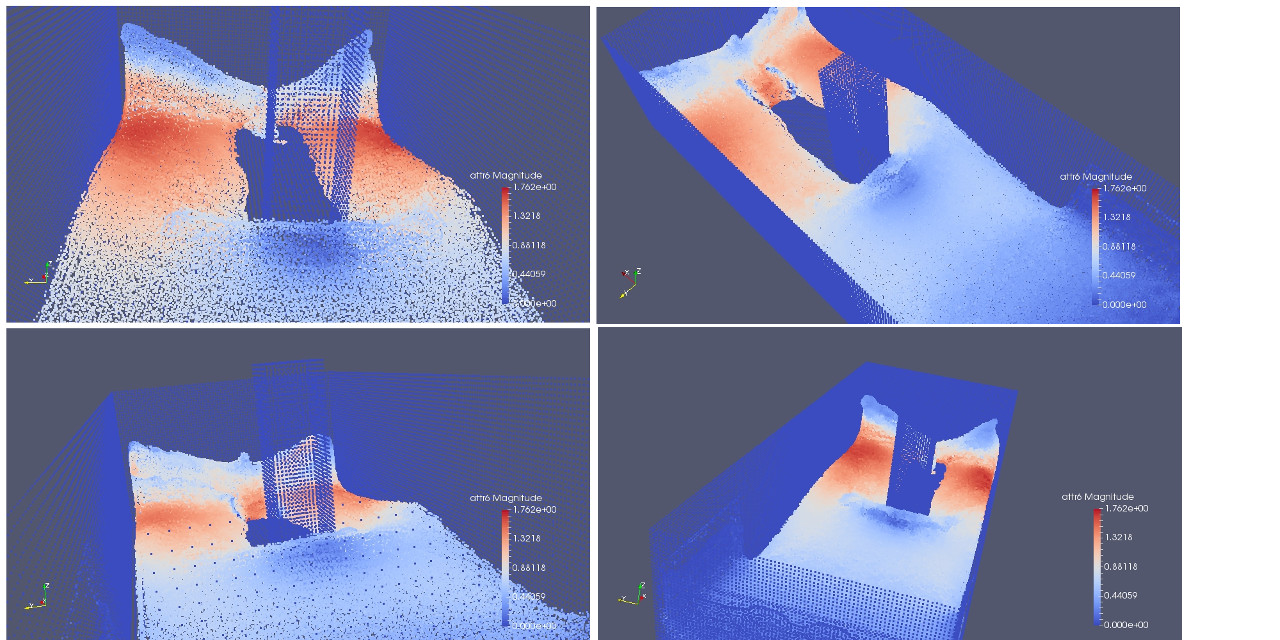
This example show the classical SPH Dam break simulation with Load Balancing and Dynamic load balancing. With Load balancing and Dynamic load balancing we indicate the possibility of the system to re-adapt the domain decomposition to keep all the processor load and reduce idle time.

Simulation video 1

Simulation video 2

Simulation dynamic load balancing video 1

Simulation dynamic load balancing video 2

Simulation countour prospective 1

Simulation countour prospective 2

Simulation countour prospective 3

Inclusion

In order to use distributed vectors in our code we have to include the file Vector/vector_dist.hpp we also include DrawParticles that has nice utilities to draw particles in parallel accordingly to simple shapes

#include "Vector/vector_dist.hpp"
#include <math.h>
#include "Draw/DrawParticles.hpp"

SPH simulation

The SPH formulation used in this example code follow these equations

\(\frac{dv_a}{dt} = - \sum_{b = NN(a) } m_b \left(\frac{P_a + P_b}{\rho_a \rho_b} + \Pi_{ab} \right) \nabla_{a} W_{ab} + g \tag{1} \)

\(\frac{d\rho_a}{dt} = \sum_{b = NN(a) } m_b v_{ab} \cdot \nabla_{a} W_{ab} \tag{2} \)

\( P_a = b \left[ \left( \frac{\rho_a}{\rho_{0}} \right)^{\gamma} - 1 \right] \tag{3} \)

with

\( \Pi_{ab} = \begin{cases} - \frac {\alpha \bar{c_{ab}} \mu_{ab} }{\bar{\rho_{ab}} } & v_{ab} \cdot r_{ab} > 0 \\ 0 & v_{ab} \cdot r_{ab} < 0 \end{cases} \tag{4}\)

and the constants defined as

\( b = \frac{c_{s}^{2} \rho_0}{\gamma} \tag{5} \)

\( c_s = \sqrt{g \cdot h_{swl}} \tag{6} \)

While the particle kernel support is given by

\( H = \sqrt{3 \cdot dp} \tag{7} \)

Explain the equations is out of the context of this tutorial. An introduction can be found regarding SPH in general in the original Monghagan SPH paper. In this example we use the sligtly modified version used by Dual-SPH (http://www.dual.sphysics.org/). A summary of the equation and constants can be founded in their User Manual and the XML user Manual.

SPH simulation

Based on the equation reported before several constants must be defined.

 
// A constant to indicate boundary particles
#define BOUNDARY 0
 
// A constant to indicate fluid particles
#define FLUID 1
 
// initial spacing between particles dp in the formulas
const double dp = 0.0085;
// Maximum height of the fluid water
// is going to be calculated and filled later on
double h_swl = 0.0;
 
// c_s in the formulas (constant used to calculate the sound speed)
const double coeff_sound = 20.0;
 
// gamma in the formulas
const double gamma_ = 7.0;
 
// sqrt(3.0*dp*dp) support of the kernel
const double H = 0.0147224318643;
 
// Eta in the formulas
const double Eta2 = 0.01 * H*H;
 
// alpha in the formula
const double visco = 0.1;
 
// cbar in the formula (calculated later)
double cbar = 0.0;
 
// Mass of the fluid particles
const double MassFluid = 0.000614125;
 
// Mass of the boundary particles
const double MassBound = 0.000614125;
 
// End simulation time
#ifdef TEST_RUN
const double t_end = 0.001;
#else
const double t_end = 1.5;
#endif
 
// Gravity acceleration
const double gravity = 9.81;
 
// Reference densitu 1000Kg/m^3
const double rho_zero = 1000.0;
 
// Filled later require h_swl, it is b in the formulas
double B = 0.0;
 
// Constant used to define time integration
const double CFLnumber = 0.2;
 
// Minimum T
const double DtMin = 0.00001;
 
// Minimum Rho allowed
const double RhoMin = 700.0;
 
// Maximum Rho allowed
const double RhoMax = 1300.0;
 
// Filled in initialization
double max_fluid_height = 0.0;
 
// Properties
 
// FLUID or BOUNDARY
const size_t type = 0;
 
// Density
const int rho = 1;
 
// Density at step n-1
const int rho_prev = 2;
 
// Pressure
const int Pressure = 3;
 
// Delta rho calculated in the force calculation
const int drho = 4;
 
// calculated force
const int force = 5;
 
// velocity
const int velocity = 6;
 
// velocity at previous step
const int velocity_prev = 7;
 

Equation of state

This function implement the formula 3 in the set of equations. It calculate the pressure of each particle based on the local density of each particle.

 
 
inline void EqState(particles & vd)
{
    auto it = vd.getDomainIterator();
 
    while (it.isNext())
    {
        auto a = it.get();
 
        double rho_a = vd.template getProp<rho>(a);
        double rho_frac = rho_a / rho_zero;
 
        vd.template getProp<Pressure>(a) = B*( rho_frac*rho_frac*rho_frac*rho_frac*rho_frac*rho_frac*rho_frac - 1.0);
 
        ++it;
    }
}
 

Cubic SPH kernel and derivatives

This function define the Cubic kernel or \( W_{ab} \). The cubic kernel is defined as

\( \begin{cases} 1.0 - \frac{3}{2} q^2 + \frac{3}{4} q^3 & 0 < q < 1 \\ (2 - q)^3 & 1 < q < 2 \\ 0 & q > 2 \end{cases} \)

 
const double a2 = 1.0/M_PI/H/H/H;
 
inline double Wab(double r)
{
    r /= H;
 
    if (r < 1.0)
        return (1.0 - 3.0/2.0*r*r + 3.0/4.0*r*r*r)*a2;
    else if (r < 2.0)
        return (1.0/4.0*(2.0 - r*r)*(2.0 - r*r)*(2.0 - r*r))*a2;
    else
        return 0.0;
}
 

This function define the gradient of the Cubic kernel function \( W_{ab} \).

\( \nabla W_{ab} = \beta (x,y,z) \)

\( \beta = \begin{cases} (c_1 q + d_1 q^2) & 0 < q < 1 \\ c_2 (2 - q)^2 & 1 < q < 2 \end{cases} \)

 
const double c1 = -3.0/M_PI/H/H/H/H;
const double d1 = 9.0/4.0/M_PI/H/H/H/H;
const double c2 = -3.0/4.0/M_PI/H/H/H/H;
const double a2_4 = 0.25*a2;
// Filled later
double W_dap = 0.0;
 
inline void DWab(Point<3,double> & dx, Point<3,double> & DW, double r, bool print)
{
    const double qq=r/H;
 
    double qq2 = qq * qq;
    double fac1 = (c1*qq + d1*qq2)/r;
    double b1 = (qq < 1.0)?1.0f:0.0f;
 
    double wqq = (2.0 - qq);
    double fac2 = c2 * wqq * wqq / r;
    double b2 = (qq >= 1.0 && qq < 2.0)?1.0f:0.0f;
 
    double factor = (b1*fac1 + b2*fac2);
 
    DW.get(0) = factor * dx.get(0);
    DW.get(1) = factor * dx.get(1);
    DW.get(2) = factor * dx.get(2);
}
 

Tensile correction

This function define the Tensile term. An explanation of the Tensile term is out of the context of this tutorial, but in brief is an additional repulsive term that avoid the particles to get too near. Can be considered at small scale like a repulsive force that avoid particles to get too close like the Lennard-Jhonned potential at atomistic level. A good reference is the Monaghan paper "SPH without a Tensile Instability"

 
// Tensile correction
inline double Tensile(double r, double rhoa, double rhob, double prs1, double prs2)
{
    const double qq=r/H;
    //-Cubic Spline kernel
    double wab;
    if(r>H)
    {
        double wqq1=2.0f-qq;
        double wqq2=wqq1*wqq1;
 
        wab=a2_4*(wqq2*wqq1);
    }
    else
    {
        double wqq2=qq*qq;
        double wqq3=wqq2*qq;
 
        wab=a2*(1.0f-1.5f*wqq2+0.75f*wqq3);
    }
 
    //-Tensile correction.
    double fab=wab*W_dap;
    fab*=fab; fab*=fab; //fab=fab^4
    const double tensilp1=(prs1/(rhoa*rhoa))*(prs1>0? 0.01: -0.2);
    const double tensilp2=(prs2/(rhob*rhob))*(prs2>0? 0.01: -0.2);
 
    return (fab*(tensilp1+tensilp2));
}
 

Viscous term

This function implement the viscous term \( \Pi_{ab} \)

 
inline double Pi(const Point<3,double> & dr, double rr2, Point<3,double> & dv, double rhoa, double rhob, double massb, double & visc)
{
    const double dot = dr.get(0)*dv.get(0) + dr.get(1)*dv.get(1) + dr.get(2)*dv.get(2);
    const double dot_rr2 = dot/(rr2+Eta2);
    visc=std::max(dot_rr2,visc);
 
    if(dot < 0)
    {
        const float amubar=H*dot_rr2;
        const float robar=(rhoa+rhob)*0.5f;
        const float pi_visc=(-visco*cbar*amubar/robar);
 
        return pi_visc;
    }
    else
        return 0.0;
}
 

Force calculation

Calculate forces. It calculate equation 1 and 2 in the set of formulas

 
template<typename CellList> inline void calc_forces(particles & vd, CellList & NN, double & max_visc)
{
    auto part = vd.getDomainIterator();
 
    // Update the cell-list
    vd.updateCellList(NN);
 
    // For each particle ...
    while (part.isNext())
    {
        // ... a
        auto a = part.get();
 
        // Get the position xp of the particle
        Point<3,double> xa = vd.getPos(a);
 
        // Take the mass of the particle dependently if it is FLUID or BOUNDARY
        double massa = (vd.getProp<type>(a) == FLUID)?MassFluid:MassBound;
 
        // Get the density of the of the particle a
        double rhoa = vd.getProp<rho>(a);
 
        // Get the pressure of the particle a
        double Pa = vd.getProp<Pressure>(a);
 
        // Get the Velocity of the particle a
        Point<3,double> va = vd.getProp<velocity>(a);
 
        // Reset the force counter (- gravity on zeta direction)
        vd.template getProp<force>(a)[0] = 0.0;
        vd.template getProp<force>(a)[1] = 0.0;
        vd.template getProp<force>(a)[2] = -gravity;
        vd.template getProp<drho>(a) = 0.0;
 
        // We threat FLUID particle differently from BOUNDARY PARTICLES ...
        if (vd.getProp<type>(a) != FLUID)
        {
            // If it is a boundary particle calculate the delta rho based on equation 2
            // This require to run across the neighborhoods particles of a
            auto Np = NN.template getNNIterator<NO_CHECK>(NN.getCell(vd.getPos(a)));
 
            // For each neighborhood particle
            while (Np.isNext() == true)
            {
                // ... q
                auto b = Np.get();
 
                // Get the position xp of the particle
                Point<3,double> xb = vd.getPos(b);
 
                // if (p == q) skip this particle
                if (a.getKey() == b)    {++Np; continue;};
 
                // get the mass of the particle
                double massb = (vd.getProp<type>(b) == FLUID)?MassFluid:MassBound;
 
                // Get the velocity of the particle b
                Point<3,double> vb = vd.getProp<velocity>(b);
 
                // Get the pressure and density of particle b
                double Pb = vd.getProp<Pressure>(b);
                double rhob = vd.getProp<rho>(b);
 
                // Get the distance between p and q
                Point<3,double> dr = xa - xb;
                // take the norm of this vector
                double r2 = norm2(dr);
 
                // If the particles interact ...
                if (r2 < 4.0*H*H)
                {
                    // ... calculate delta rho
                    double r = sqrt(r2);
 
                    Point<3,double> dv = va - vb;
 
                    Point<3,double> DW;
                    DWab(dr,DW,r,false);
 
                    const double dot = dr.get(0)*dv.get(0) + dr.get(1)*dv.get(1) + dr.get(2)*dv.get(2);
                    const double dot_rr2 = dot/(r2+Eta2);
                    max_visc=std::max(dot_rr2,max_visc);
 
                    vd.getProp<drho>(a) += massb*(dv.get(0)*DW.get(0)+dv.get(1)*DW.get(1)+dv.get(2)*DW.get(2));
                }
 
                ++Np;
            }
        }
        else
        {
            // If it is a fluid particle calculate based on equation 1 and 2
 
            // Get an iterator over the neighborhood particles of p
            auto Np = NN.template getNNIterator<NO_CHECK>(NN.getCell(vd.getPos(a)));
 
            // For each neighborhood particle
            while (Np.isNext() == true)
            {
                // ... q
                auto b = Np.get();
 
                // Get the position xp of the particle
                Point<3,double> xb = vd.getPos(b);
 
                // if (p == q) skip this particle
                if (a.getKey() == b)    {++Np; continue;};
 
                double massb = (vd.getProp<type>(b) == FLUID)?MassFluid:MassBound;
                Point<3,double> vb = vd.getProp<velocity>(b);
                double Pb = vd.getProp<Pressure>(b);
                double rhob = vd.getProp<rho>(b);
 
                // Get the distance between p and q
                Point<3,double> dr = xa - xb;
                // take the norm of this vector
                double r2 = norm2(dr);
 
                // if they interact
                if (r2 < 4.0*H*H)
                {
                    double r = sqrt(r2);
 
                    Point<3,double> v_rel = va - vb;
 
                    Point<3,double> DW;
                    DWab(dr,DW,r,false);
 
                    double factor = - massb*((vd.getProp<Pressure>(a) + vd.getProp<Pressure>(b)) / (rhoa * rhob) + Tensile(r,rhoa,rhob,Pa,Pb) + Pi(dr,r2,v_rel,rhoa,rhob,massb,max_visc));
 
                    vd.getProp<force>(a)[0] += factor * DW.get(0);
                    vd.getProp<force>(a)[1] += factor * DW.get(1);
                    vd.getProp<force>(a)[2] += factor * DW.get(2);
 
                    vd.getProp<drho>(a) += massb*(v_rel.get(0)*DW.get(0)+v_rel.get(1)*DW.get(1)+v_rel.get(2)*DW.get(2));
                }
 
                ++Np;
            }
        }
 
        ++part;
    }
}
 

Integration and dynamic time integration

This function calculate the Maximum acceleration and velocity across the particles. It is used to calculate a dynamic time-stepping.

 
void max_acceleration_and_velocity(particles & vd, double & max_acc, double & max_vel)
{
    // Calculate the maximum acceleration
    auto part = vd.getDomainIterator();
 
    while (part.isNext())
    {
        auto a = part.get();
 
        Point<3,double> acc(vd.getProp<force>(a));
        double acc2 = norm2(acc);
 
        Point<3,double> vel(vd.getProp<velocity>(a));
        double vel2 = norm2(vel);
 
        if (vel2 >= max_vel)
            max_vel = vel2;
 
        if (acc2 >= max_acc)
            max_acc = acc2;
 
        ++part;
    }
    max_acc = sqrt(max_acc);
    max_vel = sqrt(max_vel);
 
    Vcluster<> & v_cl = create_vcluster();
    v_cl.max(max_acc);
    v_cl.max(max_vel);
    v_cl.execute();
}
 

In this example we are using Dynamic time-stepping. The Dynamic time stepping is calculated with the Courant-Friedrich-Lewy condition. See Monaghan 1992 "Smoothed Particle Hydrodynamic"

\( \delta t = CFL \cdot min(t_f,t_{cv}) \)

where

\( \delta t_f = min \sqrt{h/f_a}\)

\( \delta t_{cv} = min \frac{h}{c_s + max \left| \frac{hv_{ab} \cdot r_{ab}}{r_{ab}^2} \right|} \)

 
double calc_deltaT(particles & vd, double ViscDtMax)
{
    double Maxacc = 0.0;
    double Maxvel = 0.0;
    max_acceleration_and_velocity(vd,Maxacc,Maxvel);
 
    //-dt1 depends on force per unit mass.
    const double dt_f = (Maxacc)?sqrt(H/Maxacc):std::numeric_limits<int>::max();
 
    //-dt2 combines the Courant and the viscous time-step controls.
    const double dt_cv = H/(std::max(cbar,Maxvel*10.) + H*ViscDtMax);
 
    //-dt new value of time step.
    double dt=double(CFLnumber)*std::min(dt_f,dt_cv);
    if(dt<double(DtMin))
        dt=double(DtMin);
 
    return dt;
}
 

This function perform verlet integration accordingly to the Verlet time stepping scheme

\( v_a^{n+1} = v_a^{n-1} + 2 \delta t F_a^{n} \)

\( r_a^{n+1} = \delta t V_a^n + 0.5 \delta t^2 F_a^n \)

\( \rho_a^{n+1} = \rho_a^{n-1} + 2 \delta t D_a^n \)

Every N Verlet steps the euler stepping scheme is choosen to avoid instabilities

\( v_a^{n+1} = v_a^{n} + \delta t F_a^n \)

\( r_a^{n+1} = r_a^{n} + \delta t V_a^n + \frac{1}{2} \delta t^2 F_a^n \)

\( \rho_a^{n+1} = \rho_a^n + \delta t D_a^n \)

This function also check that no particles go outside the simulation domain or their density go dangerously out of range. If a particle go out of range is removed from the simulation

 
openfpm::vector<size_t> to_remove;
 
size_t cnt = 0;
 
void verlet_int(particles & vd, double dt)
{
    // list of the particle to remove
    to_remove.clear();
 
    // particle iterator
    auto part = vd.getDomainIterator();
 
    double dt205 = dt*dt*0.5;
    double dt2 = dt*2.0;
 
    // For each particle ...
    while (part.isNext())
    {
        // ... a
        auto a = part.get();
 
        // if the particle is boundary
        if (vd.template getProp<type>(a) == BOUNDARY)
        {
            // Update rho
            double rhop = vd.template getProp<rho>(a);
 
            // Update only the density
            vd.template getProp<velocity>(a)[0] = 0.0;
            vd.template getProp<velocity>(a)[1] = 0.0;
            vd.template getProp<velocity>(a)[2] = 0.0;
            double rhonew = vd.template getProp<rho_prev>(a) + dt2*vd.template getProp<drho>(a);
            vd.template getProp<rho>(a) = (rhonew < rho_zero)?rho_zero:rhonew;
 
            vd.template getProp<rho_prev>(a) = rhop;
 
            ++part;
            continue;
        }
 
        //-Calculate displacement and update position / Calcula desplazamiento y actualiza posicion.
        double dx = vd.template getProp<velocity>(a)[0]*dt + vd.template getProp<force>(a)[0]*dt205;
        double dy = vd.template getProp<velocity>(a)[1]*dt + vd.template getProp<force>(a)[1]*dt205;
        double dz = vd.template getProp<velocity>(a)[2]*dt + vd.template getProp<force>(a)[2]*dt205;
 
        vd.getPos(a)[0] += dx;
        vd.getPos(a)[1] += dy;
        vd.getPos(a)[2] += dz;
 
        double velX = vd.template getProp<velocity>(a)[0];
        double velY = vd.template getProp<velocity>(a)[1];
        double velZ = vd.template getProp<velocity>(a)[2];
        double rhop = vd.template getProp<rho>(a);
 
        vd.template getProp<velocity>(a)[0] = vd.template getProp<velocity_prev>(a)[0] + vd.template getProp<force>(a)[0]*dt2;
        vd.template getProp<velocity>(a)[1] = vd.template getProp<velocity_prev>(a)[1] + vd.template getProp<force>(a)[1]*dt2;
        vd.template getProp<velocity>(a)[2] = vd.template getProp<velocity_prev>(a)[2] + vd.template getProp<force>(a)[2]*dt2;
        vd.template getProp<rho>(a) = vd.template getProp<rho_prev>(a) + dt2*vd.template getProp<drho>(a);
 
        // Check if the particle go out of range in space and in density
        if (vd.getPos(a)[0] <  0.000263878 || vd.getPos(a)[1] < 0.000263878 || vd.getPos(a)[2] < 0.000263878 ||
            vd.getPos(a)[0] >  0.000263878+1.59947 || vd.getPos(a)[1] > 0.000263878+0.672972 || vd.getPos(a)[2] > 0.000263878+0.903944 ||
            vd.template getProp<rho>(a) < RhoMin || vd.template getProp<rho>(a) > RhoMax)
        {
                       to_remove.add(a.getKey());
        }
 
        vd.template getProp<velocity_prev>(a)[0] = velX;
        vd.template getProp<velocity_prev>(a)[1] = velY;
        vd.template getProp<velocity_prev>(a)[2] = velZ;
        vd.template getProp<rho_prev>(a) = rhop;
 
        ++part;
    }
 
    // remove the particles
    vd.remove(to_remove,0);
 
    // increment the iteration counter
    cnt++;
}
 
void euler_int(particles & vd, double dt)
{
    // list of the particle to remove
    to_remove.clear();
 
    // particle iterator
    auto part = vd.getDomainIterator();
 
    double dt205 = dt*dt*0.5;
    double dt2 = dt*2.0;
 
    // For each particle ...
    while (part.isNext())
    {
        // ... a
        auto a = part.get();
 
        // if the particle is boundary
        if (vd.template getProp<type>(a) == BOUNDARY)
        {
            // Update rho
            double rhop = vd.template getProp<rho>(a);
 
            // Update only the density
            vd.template getProp<velocity>(a)[0] = 0.0;
            vd.template getProp<velocity>(a)[1] = 0.0;
            vd.template getProp<velocity>(a)[2] = 0.0;
            double rhonew = vd.template getProp<rho>(a) + dt*vd.template getProp<drho>(a);
            vd.template getProp<rho>(a) = (rhonew < rho_zero)?rho_zero:rhonew;
 
            vd.template getProp<rho_prev>(a) = rhop;
 
            ++part;
            continue;
        }
 
        //-Calculate displacement and update position / Calcula desplazamiento y actualiza posicion.
        double dx = vd.template getProp<velocity>(a)[0]*dt + vd.template getProp<force>(a)[0]*dt205;
        double dy = vd.template getProp<velocity>(a)[1]*dt + vd.template getProp<force>(a)[1]*dt205;
        double dz = vd.template getProp<velocity>(a)[2]*dt + vd.template getProp<force>(a)[2]*dt205;
 
        vd.getPos(a)[0] += dx;
        vd.getPos(a)[1] += dy;
        vd.getPos(a)[2] += dz;
 
        double velX = vd.template getProp<velocity>(a)[0];
        double velY = vd.template getProp<velocity>(a)[1];
        double velZ = vd.template getProp<velocity>(a)[2];
        double rhop = vd.template getProp<rho>(a);
 
        vd.template getProp<velocity>(a)[0] = vd.template getProp<velocity>(a)[0] + vd.template getProp<force>(a)[0]*dt;
        vd.template getProp<velocity>(a)[1] = vd.template getProp<velocity>(a)[1] + vd.template getProp<force>(a)[1]*dt;
        vd.template getProp<velocity>(a)[2] = vd.template getProp<velocity>(a)[2] + vd.template getProp<force>(a)[2]*dt;
        vd.template getProp<rho>(a) = vd.template getProp<rho>(a) + dt*vd.template getProp<drho>(a);
 
        // Check if the particle go out of range in space and in density
        if (vd.getPos(a)[0] <  0.000263878 || vd.getPos(a)[1] < 0.000263878 || vd.getPos(a)[2] < 0.000263878 ||
            vd.getPos(a)[0] >  0.000263878+1.59947 || vd.getPos(a)[1] > 0.000263878+0.672972 || vd.getPos(a)[2] > 0.000263878+0.903944 ||
            vd.template getProp<rho>(a) < RhoMin || vd.template getProp<rho>(a) > RhoMax)
        {
                       to_remove.add(a.getKey());
        }
 
        vd.template getProp<velocity_prev>(a)[0] = velX;
        vd.template getProp<velocity_prev>(a)[1] = velY;
        vd.template getProp<velocity_prev>(a)[2] = velZ;
        vd.template getProp<rho_prev>(a) = rhop;
 
        ++part;
    }
 
    // remove the particles
    vd.remove(to_remove,0);
 
    // increment the iteration counter
    cnt++;
}
 

Probes/sensors

This function show how to create a pressure sensor/probe on a set of specified points. To do this from the cell-list we just get an iterator across the neighborhood points of the sensors and we calculate the pressure profile. On the other hand because the sensor is in the processor domain of only one processor, only one processor must do this calculation. We will use the function isLocal to determine which processor contain the probe and only such processor will do the calculation.

Warning

This type of calculation is suitable if the number of probes is small (like 10) and pressure is not calculated every time step. In case the number of probes is comparable to the number of particles or the pressure is calculated every time-step than we suggest to create a set of "probe" particles

 
template<typename Vector, typename CellList>
inline void sensor_pressure(Vector & vd,
                            CellList & NN,
                            openfpm::vector<openfpm::vector<double>> & press_t,
                            openfpm::vector<Point<3,double>> & probes)
{
    Vcluster<> & v_cl = create_vcluster();
 
    press_t.add();
 
    for (size_t i = 0 ; i < probes.size() ; i++)
    {
        float press_tmp = 0.0f;
        float tot_ker = 0.0;
 
        // if the probe is inside the processor domain
        if (vd.getDecomposition().isLocal(probes.get(i)) == true)
        {
            // Get the position of the probe i
            Point<3,double> xp = probes.get(i);
 
            // get the iterator over the neighbohood particles of the probes position
            auto itg = NN.template getNNIterator<NO_CHECK>(NN.getCell(probes.get(i)));
            while (itg.isNext())
            {
                auto q = itg.get();
 
                // Only the fluid particles are importants
                if (vd.template getProp<type>(q) != FLUID)
                {
                    ++itg;
                    continue;
                }
 
                // Get the position of the neighborhood particle q
                Point<3,double> xq = vd.getPos(q);
 
                // Calculate the contribution of the particle to the pressure
                // of the probe
                double r = sqrt(norm2(xp - xq));
 
                double ker = Wab(r) * (MassFluid / rho_zero);
 
                // Also keep track of the calculation of the summed
                // kernel
                tot_ker += ker;
 
                // Add the total pressure contribution
                press_tmp += vd.template getProp<Pressure>(q) * ker;
 
                // next neighborhood particle
                ++itg;
            }
 
            // We calculate the pressure normalizing the
            // sum over all kernels
            if (tot_ker == 0.0)
                press_tmp = 0.0;
            else
                press_tmp = 1.0 / tot_ker * press_tmp;
 
        }
 
        // This is not necessary in principle, but if you
        // want to make all processor aware of the history of the calculated
        // pressure we have to execute this
        v_cl.sum(press_tmp);
        v_cl.execute();
 
        // We add the calculated pressure into the history
        press_t.last().add(press_tmp);
    }
}
 

Main function

Here we Initialize the library, we create a Box that define our domain, boundary conditions and ghost. We also create a vector that contain two probes to measure pressure

See also

Initialization

 
    // initialize the library
    openfpm_init(&argc,&argv);
 
    // It contain for each time-step the value detected by the probes
    openfpm::vector<openfpm::vector<double>> press_t;
    openfpm::vector<Point<3,double>> probes;
 
    probes.add({0.8779,0.3,0.02});
    probes.add({0.754,0.31,0.02});
 
    // Here we define our domain a 2D box with internals from 0 to 1.0 for x and y
    Box<3,double> domain({-0.05,-0.05,-0.05},{1.7010,0.7065,0.5025});
    size_t sz[3] = {207,90,66};
 
    // Fill W_dap
    W_dap = 1.0/Wab(H/1.5);
 
    // Here we define the boundary conditions of our problem
    size_t bc[3]={NON_PERIODIC,NON_PERIODIC,NON_PERIODIC};
 
    // extended boundary around the domain, and the processor domain
    Ghost<3,double> g(2*H);
    

Vector create

Here we define a distributed vector in 3D, we use the particles type that we defined previously. Each particle contain the following properties

• type Type of the particle
• rho Density of the particle
• rho_prev Density at previous timestep
• Pressure Pressure of the particle
• drho Derivative of the density over time
• force acceleration of the particles
• velocity velocity of the particles
• velocity_prev velocity of the particles at previous time-step

In this case the vector contain 0 particles initially

See also

Vector instantiation

The option DEC_GRAN(512) is related to the Load-Balancing decomposition granularity. It indicate that the space must be decomposed by at least

\( N_{subsub} = 512 \cdot N_p \)

Where \( N_{subsub} \) is the number of sub-sub-domain in which the space must be decomposed and \( N_p \) is the number of processors. (The concept of sub-sub-domain will be explained leter)

 
    particles vd(0,domain,bc,g,DEC_GRAN(512));
 

 
// Type of the vector containing particles
typedef vector_dist<3,double,aggregate<size_t,double,  double,    double,     double,     double[3], double[3], double[3]>> particles;
//                                       |      |        |          |            |            |         |            |
//                                       |      |        |          |            |            |         |            |
//                                     type   density   density    Pressure    delta       force     velocity    velocity
//                                                      at n-1                 density                           at n - 1
 

Draw particles and initialization

In this part we initialize the problem creating particles. In order to do it we use the class DrawParticles. Because some of the simulation constants require the maximum height \( h_{swl} \) of the fluid to be calculated and the maximum fluid height is determined at runtime, some of the constants just after we create the fluid particles

Draw Fluid

The Function DrawParticles::DrawBox return an iterator that can be used to create particle in a predefined box (smaller than the simulation domain) with a predefined spacing. We start drawing the fluid particles, the initial pressure is initialized accordingly to the Hydrostatic pressure given by:

\( P = \rho_{0} g (h_{max} - z) \)

Where \( h_{max} \) is the maximum height of the fluid. The density instead is given by the equation (3). Assuming \( \rho \) constant to \( \rho_{0} \) in the Hydrostatic equation is a good approximation. Velocity is initialized to zero.

See also

Vector instantiation

 
    // You can ignore all these dp/2.0 is a trick to reach the same initialization
    // of Dual-SPH that use a different criteria to draw particles
    Box<3,double> fluid_box({dp/2.0,dp/2.0,dp/2.0},{0.4+dp/2.0,0.67-dp/2.0,0.3+dp/2.0});
 
    // return an iterator to the fluid particles to add to vd
    auto fluid_it = DrawParticles::DrawBox(vd,sz,domain,fluid_box);
 
    // here we fill some of the constants needed by the simulation
    max_fluid_height = fluid_it.getBoxMargins().getHigh(2);
    h_swl = fluid_it.getBoxMargins().getHigh(2) - fluid_it.getBoxMargins().getLow(2);
    B = (coeff_sound)*(coeff_sound)*gravity*h_swl*rho_zero / gamma_;
    cbar = coeff_sound * sqrt(gravity * h_swl);
 
    // for each particle inside the fluid box ...
    while (fluid_it.isNext())
    {
        // ... add a particle ...
        vd.add();
 
        // ... and set it position ...
        vd.getLastPos()[0] = fluid_it.get().get(0);
        vd.getLastPos()[1] = fluid_it.get().get(1);
        vd.getLastPos()[2] = fluid_it.get().get(2);
 
        // and its type.
        vd.template getLastProp<type>() = FLUID;
 
        // We also initialize the density of the particle and the hydro-static pressure given by
        //
        // rho_zero*g*h = P
        //
        // rho_p = (P/B + 1)^(1/Gamma) * rho_zero
        //
 
        vd.template getLastProp<Pressure>() = rho_zero * gravity *  (max_fluid_height - fluid_it.get().get(2));
 
        vd.template getLastProp<rho>() = pow(vd.template getLastProp<Pressure>() / B + 1, 1.0/gamma_) * rho_zero;
        vd.template getLastProp<rho_prev>() = vd.template getLastProp<rho>();
        vd.template getLastProp<velocity>()[0] = 0.0;
        vd.template getLastProp<velocity>()[1] = 0.0;
        vd.template getLastProp<velocity>()[2] = 0.0;
 
        vd.template getLastProp<velocity_prev>()[0] = 0.0;
        vd.template getLastProp<velocity_prev>()[1] = 0.0;
        vd.template getLastProp<velocity_prev>()[2] = 0.0;
 
        // next fluid particle
        ++fluid_it;
    }
 

Draw Recipient

Here we draw the recipient using the function DrawParticles::DrawSkin. This function can draw a set of particles inside a box A removed of a second box or an array of boxes. So all the particles in the area included in the area A - B - C. There is no restriction that B or C must be included into A.

In this case A is the box defining the recipient, B is the box cutting out the internal part of the recipient, C is the hole where we will place the obstacle. Because we use Dynamic boundary condition (DBC) we initialize the density to \( \rho_{0} \). It will be update over time according to equation (3) to keep the particles confined.

 
    // Recipient
    Box<3,double> recipient1({0.0,0.0,0.0},{1.6+dp/2.0,0.67+dp/2.0,0.4+dp/2.0});
    Box<3,double> recipient2({dp,dp,dp},{1.6-dp/2.0,0.67-dp/2.0,0.4+dp/2.0});
 
    Box<3,double> obstacle1({0.9,0.24-dp/2.0,0.0},{1.02+dp/2.0,0.36,0.45+dp/2.0});
    Box<3,double> obstacle2({0.9+dp,0.24+dp/2.0,0.0},{1.02-dp/2.0,0.36-dp,0.45-dp/2.0});
    Box<3,double> obstacle3({0.9+dp,0.24,0.0},{1.02,0.36,0.45});
 
    openfpm::vector<Box<3,double>> holes;
    holes.add(recipient2);
    holes.add(obstacle1);
    auto bound_box = DrawParticles::DrawSkin(vd,sz,domain,holes,recipient1);
 
    while (bound_box.isNext())
    {
        vd.add();
 
        vd.getLastPos()[0] = bound_box.get().get(0);
        vd.getLastPos()[1] = bound_box.get().get(1);
        vd.getLastPos()[2] = bound_box.get().get(2);
 
        vd.template getLastProp<type>() = BOUNDARY;
        vd.template getLastProp<rho>() = rho_zero;
        vd.template getLastProp<rho_prev>() = rho_zero;
        vd.template getLastProp<velocity>()[0] = 0.0;
        vd.template getLastProp<velocity>()[1] = 0.0;
        vd.template getLastProp<velocity>()[2] = 0.0;
 
        vd.template getLastProp<velocity_prev>()[0] = 0.0;
        vd.template getLastProp<velocity_prev>()[1] = 0.0;
        vd.template getLastProp<velocity_prev>()[2] = 0.0;
 
        ++bound_box;
    }
 

Draw Obstacle

Here we draw the obstacle in the same way we draw the recipient. also for the obstacle is valid the same concept of using Dynamic boundary condition (DBC)

 
    auto obstacle_box = DrawParticles::DrawSkin(vd,sz,domain,obstacle2,obstacle1);
 
    while (obstacle_box.isNext())
    {
        vd.add();
 
        vd.getLastPos()[0] = obstacle_box.get().get(0);
        vd.getLastPos()[1] = obstacle_box.get().get(1);
        vd.getLastPos()[2] = obstacle_box.get().get(2);
 
        vd.template getLastProp<type>() = BOUNDARY;
        vd.template getLastProp<rho>() = rho_zero;
        vd.template getLastProp<rho_prev>() = rho_zero;
        vd.template getLastProp<velocity>()[0] = 0.0;
        vd.template getLastProp<velocity>()[1] = 0.0;
        vd.template getLastProp<velocity>()[2] = 0.0;
 
        vd.template getLastProp<velocity_prev>()[0] = 0.0;
        vd.template getLastProp<velocity_prev>()[1] = 0.0;
        vd.template getLastProp<velocity_prev>()[2] = 0.0;
 
        ++obstacle_box;
    }
 
    vd.map();
 

Load balancing and Dynamic load balancing

Load Balancing

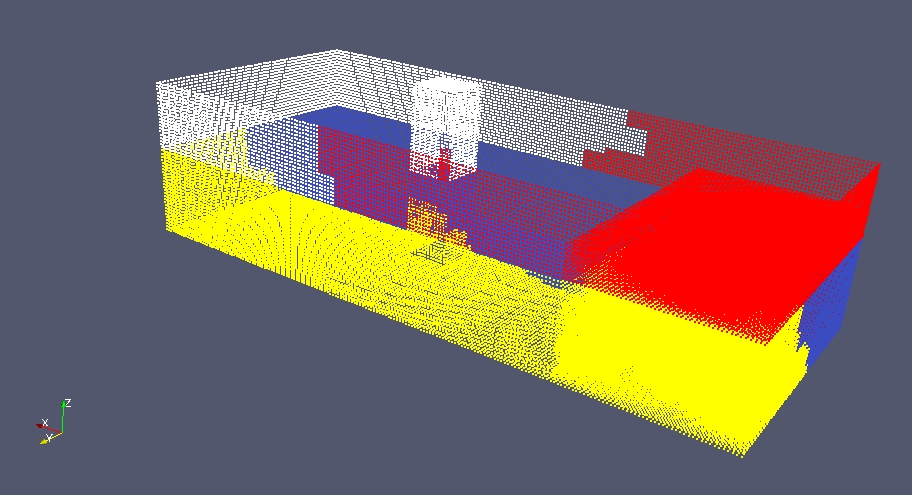
If at this point we output the particles and we visualize where they are accordingly to their processor id we can easily see that particles are distributed unevenly. The processor that has particles in white has few particles and all of them are non fluid. This mean that it will be almost in idle. This situation is not ideal

In order to reach an optimal situation we have to distribute the particles to reach a balanced situation. To do this we have to set the computation of each sub-sub-domain, redecompose the space and distribute the particles accordingly to this new configuration. To do this we need a model. A model specify how to set the computational cost for each sub-sub-domains (for example it specify if the computational cost to process a sub-sub-domain is quadratic or linear with the number of particles ...). A model look like this.

 
struct ModelCustom
{
    template<typename Decomposition, typename vector> inline void addComputation(Decomposition & dec,
                                                                                 vector & vd,
                                                                                 size_t v,
                                                                                 size_t p)
    {
        if (vd.template getProp<type>(p) == FLUID)
            dec.addComputationCost(v,4);
        else
            dec.addComputationCost(v,3);
    }
 
    template<typename Decomposition> inline void applyModel(Decomposition & dec, size_t v)
    {
        dec.setSubSubDomainComputationCost(v, dec.getSubSubDomainComputationCost(v) * dec.getSubSubDomainComputationCost(v));
    }
 
    double distributionTol()
    {
        return 1.01;
    }
};
 

Setting the the computational cost on sub-sub-domains is performed running across the particles. For each one of them, it is calculated on which sub-sub-domain it belong. Than the function addComputation is called. Inside this call we can set the weight in the way we prefer. In this case we set the weight as:

\( w_v = 4 N_{fluid} + 3 N_{boundary} \)

Where \( N_{fluid} \) Is the number of fluid particles in the sub-sub-domains and \( N_{boundary} \) are the number of boundary particles. For example in our ModelCustom we square this number, because the computation is proportional to the square of the number of particles in each sub-sub-domain. A second cycle is performed in order to calculate a complex function of this number (for example squaring).

Implicitly the communication cost is given by \( \frac{V_{ghost}}{V_{sub-sub}} t_s \), while the migration cost is given by \( v_{sub-sub} \). In general \( t_s \) is the number of ghost get between two rebalance. In this special case where we have two type of particles, we have two different computation for each of them, this mean that fluid particles and boundary particles has different computation cost.

After filling the computational cost based on our model we can decompose the problem in computationally equal chunk for each processor. We use the function decomposed to redecompose the space and subsequently we use the function map to redistribute the particles.

Note

All processors now has part of the fluid. It is good to note that the computationaly balanced configuration does not correspond to the evenly distributed particles to know more about that please follow the video tutorials

Dynamic load balancing the theory part1

Dynamic load balancing the theory part2

Dynamic load balancing practice part1

Dynamic load balancing practice part2

 
    // Now that we fill the vector with particles
    ModelCustom md;
 
    vd.addComputationCosts(md);
    vd.getDecomposition().decompose();
    vd.map();
 

Main Loop

The main loop do time integration. It calculate the pressure based on the density, than calculate the forces, than we calculate delta time, and finally update position and velocity. After 200 time-step we do a re-balancing. We save the configuration and we calculate the pressure on the probe position every 0.01 seconds

 
    size_t write = 0;
    size_t it = 0;
    size_t it_reb = 0;
    double t = 0.0;
    while (t <= t_end)
    {
        Vcluster<> & v_cl = create_vcluster();
        timer it_time;
 
        it_reb++;
        if (it_reb == 200)
        {
            vd.map();
 
            it_reb = 0;
            ModelCustom md;
            vd.addComputationCosts(md);
            vd.getDecomposition().decompose();
 
            if (v_cl.getProcessUnitID() == 0)
                std::cout << "REBALANCED " << std::endl;
        }
 
        vd.map();
 
        // Calculate pressure from the density
        EqState(vd);
 
        double max_visc = 0.0;
 
        vd.ghost_get<type,rho,Pressure,velocity>();
 
        // Calc forces
        calc_forces(vd,NN,max_visc);
 
        // Get the maximum viscosity term across processors
        v_cl.max(max_visc);
        v_cl.execute();
 
        // Calculate delta t integration
        double dt = calc_deltaT(vd,max_visc);
 
        // VerletStep or euler step
        it++;
        if (it < 40)
            verlet_int(vd,dt);
        else
        {
            euler_int(vd,dt);
            it = 0;
        }
 
        t += dt;
 
        if (write < t*100)
        {
            // sensor_pressure calculation require ghost and update cell-list
            vd.map();
            vd.ghost_get<type,rho,Pressure,velocity>();
            vd.updateCellList(NN);
 
            // calculate the pressure at the sensor points
            sensor_pressure(vd,NN,press_t,probes);
 
            vd.write_frame("Geometry",write);
            write++;
 
            if (v_cl.getProcessUnitID() == 0)
            {std::cout << "TIME: " << t << "  write " << it_time.getwct() << "   " << v_cl.getProcessUnitID() << "   " << cnt << "   Max visc: " << max_visc << std::endl;}
        }
        else
        {
            if (v_cl.getProcessUnitID() == 0)
            {std::cout << "TIME: " << t << "  " << it_time.getwct() << "   " << v_cl.getProcessUnitID() << "   " << cnt << "    Max visc: " << max_visc << std::endl;}
        }
    }
 

Finalize

At the very end of the program we have always de-initialize the library

 
    openfpm_finalize();
 

Full code

 
//#define SE_CLASS1
//#define STOP_ON_ERROR
 
#include "Vector/vector_dist.hpp"
#include <math.h>
#include "Draw/DrawParticles.hpp"
 
// A constant to indicate boundary particles
#define BOUNDARY 0
 
// A constant to indicate fluid particles
#define FLUID 1
 
// initial spacing between particles dp in the formulas
const double dp = 0.0085;
// Maximum height of the fluid water
// is going to be calculated and filled later on
double h_swl = 0.0;
 
// c_s in the formulas (constant used to calculate the sound speed)
const double coeff_sound = 20.0;
 
// gamma in the formulas
const double gamma_ = 7.0;
 
// sqrt(3.0*dp*dp) support of the kernel
const double H = 0.0147224318643;
 
// Eta in the formulas
const double Eta2 = 0.01 * H*H;
 
// alpha in the formula
const double visco = 0.1;
 
// cbar in the formula (calculated later)
double cbar = 0.0;
 
// Mass of the fluid particles
const double MassFluid = 0.000614125;
 
// Mass of the boundary particles
const double MassBound = 0.000614125;
 
// End simulation time
#ifdef TEST_RUN
const double t_end = 0.001;
#else
const double t_end = 1.5;
#endif
 
// Gravity acceleration
const double gravity = 9.81;
 
// Reference densitu 1000Kg/m^3
const double rho_zero = 1000.0;
 
// Filled later require h_swl, it is b in the formulas
double B = 0.0;
 
// Constant used to define time integration
const double CFLnumber = 0.2;
 
// Minimum T
const double DtMin = 0.00001;
 
// Minimum Rho allowed
const double RhoMin = 700.0;
 
// Maximum Rho allowed
const double RhoMax = 1300.0;
 
// Filled in initialization
double max_fluid_height = 0.0;
 
// Properties
 
// FLUID or BOUNDARY
const size_t type = 0;
 
// Density
const int rho = 1;
 
// Density at step n-1
const int rho_prev = 2;
 
// Pressure
const int Pressure = 3;
 
// Delta rho calculated in the force calculation
const int drho = 4;
 
// calculated force
const int force = 5;
 
// velocity
const int velocity = 6;
 
// velocity at previous step
const int velocity_prev = 7;
 
// Type of the vector containing particles
typedef vector_dist<3,double,aggregate<size_t,double,  double,    double,     double,     double[3], double[3], double[3]>> particles;
//                                       |      |        |          |            |            |         |            |
//                                       |      |        |          |            |            |         |            |
//                                     type   density   density    Pressure    delta       force     velocity    velocity
//                                                      at n-1                 density                           at n - 1
 
struct ModelCustom
{
    template<typename Decomposition, typename vector> inline void addComputation(Decomposition & dec,
                                                                                 vector & vd,
                                                                                 size_t v,
                                                                                 size_t p)
    {
        if (vd.template getProp<type>(p) == FLUID)
            dec.addComputationCost(v,4);
        else
            dec.addComputationCost(v,3);
    }
 
    template<typename Decomposition> inline void applyModel(Decomposition & dec, size_t v)
    {
        dec.setSubSubDomainComputationCost(v, dec.getSubSubDomainComputationCost(v) * dec.getSubSubDomainComputationCost(v));
    }
 
    double distributionTol()
    {
        return 1.01;
    }
};
 
inline void EqState(particles & vd)
{
    auto it = vd.getDomainIterator();
 
    while (it.isNext())
    {
        auto a = it.get();
 
        double rho_a = vd.template getProp<rho>(a);
        double rho_frac = rho_a / rho_zero;
 
        vd.template getProp<Pressure>(a) = B*( rho_frac*rho_frac*rho_frac*rho_frac*rho_frac*rho_frac*rho_frac - 1.0);
 
        ++it;
    }
}
 
const double a2 = 1.0/M_PI/H/H/H;
 
inline double Wab(double r)
{
    r /= H;
 
    if (r < 1.0)
        return (1.0 - 3.0/2.0*r*r + 3.0/4.0*r*r*r)*a2;
    else if (r < 2.0)
        return (1.0/4.0*(2.0 - r*r)*(2.0 - r*r)*(2.0 - r*r))*a2;
    else
        return 0.0;
}
 
const double c1 = -3.0/M_PI/H/H/H/H;
const double d1 = 9.0/4.0/M_PI/H/H/H/H;
const double c2 = -3.0/4.0/M_PI/H/H/H/H;
const double a2_4 = 0.25*a2;
// Filled later
double W_dap = 0.0;
 
inline void DWab(Point<3,double> & dx, Point<3,double> & DW, double r, bool print)
{
    const double qq=r/H;
 
    double qq2 = qq * qq;
    double fac1 = (c1*qq + d1*qq2)/r;
    double b1 = (qq < 1.0)?1.0f:0.0f;
 
    double wqq = (2.0 - qq);
    double fac2 = c2 * wqq * wqq / r;
    double b2 = (qq >= 1.0 && qq < 2.0)?1.0f:0.0f;
 
    double factor = (b1*fac1 + b2*fac2);
 
    DW.get(0) = factor * dx.get(0);
    DW.get(1) = factor * dx.get(1);
    DW.get(2) = factor * dx.get(2);
}
 
// Tensile correction
inline double Tensile(double r, double rhoa, double rhob, double prs1, double prs2)
{
    const double qq=r/H;
    //-Cubic Spline kernel
    double wab;
    if(r>H)
    {
        double wqq1=2.0f-qq;
        double wqq2=wqq1*wqq1;
 
        wab=a2_4*(wqq2*wqq1);
    }
    else
    {
        double wqq2=qq*qq;
        double wqq3=wqq2*qq;
 
        wab=a2*(1.0f-1.5f*wqq2+0.75f*wqq3);
    }
 
    //-Tensile correction.
    double fab=wab*W_dap;
    fab*=fab; fab*=fab; //fab=fab^4
    const double tensilp1=(prs1/(rhoa*rhoa))*(prs1>0? 0.01: -0.2);
    const double tensilp2=(prs2/(rhob*rhob))*(prs2>0? 0.01: -0.2);
 
    return (fab*(tensilp1+tensilp2));
}
 
inline double Pi(const Point<3,double> & dr, double rr2, Point<3,double> & dv, double rhoa, double rhob, double massb, double & visc)
{
    const double dot = dr.get(0)*dv.get(0) + dr.get(1)*dv.get(1) + dr.get(2)*dv.get(2);
    const double dot_rr2 = dot/(rr2+Eta2);
    visc=std::max(dot_rr2,visc);
 
    if(dot < 0)
    {
        const float amubar=H*dot_rr2;
        const float robar=(rhoa+rhob)*0.5f;
        const float pi_visc=(-visco*cbar*amubar/robar);
 
        return pi_visc;
    }
    else
        return 0.0;
}
 
template<typename CellList> inline void calc_forces(particles & vd, CellList & NN, double & max_visc)
{
    auto part = vd.getDomainIterator();
 
    // Update the cell-list
    vd.updateCellList(NN);
 
    // For each particle ...
    while (part.isNext())
    {
        // ... a
        auto a = part.get();
 
        // Get the position xp of the particle
        Point<3,double> xa = vd.getPos(a);
 
        // Take the mass of the particle dependently if it is FLUID or BOUNDARY
        double massa = (vd.getProp<type>(a) == FLUID)?MassFluid:MassBound;
 
        // Get the density of the of the particle a
        double rhoa = vd.getProp<rho>(a);
 
        // Get the pressure of the particle a
        double Pa = vd.getProp<Pressure>(a);
 
        // Get the Velocity of the particle a
        Point<3,double> va = vd.getProp<velocity>(a);
 
        // Reset the force counter (- gravity on zeta direction)
        vd.template getProp<force>(a)[0] = 0.0;
        vd.template getProp<force>(a)[1] = 0.0;
        vd.template getProp<force>(a)[2] = -gravity;
        vd.template getProp<drho>(a) = 0.0;
 
        // We threat FLUID particle differently from BOUNDARY PARTICLES ...
        if (vd.getProp<type>(a) != FLUID)
        {
            // If it is a boundary particle calculate the delta rho based on equation 2
            // This require to run across the neighborhoods particles of a
            auto Np = NN.template getNNIterator<NO_CHECK>(NN.getCell(vd.getPos(a)));
 
            // For each neighborhood particle
            while (Np.isNext() == true)
            {
                // ... q
                auto b = Np.get();
 
                // Get the position xp of the particle
                Point<3,double> xb = vd.getPos(b);
 
                // if (p == q) skip this particle
                if (a.getKey() == b)    {++Np; continue;};
 
                // get the mass of the particle
                double massb = (vd.getProp<type>(b) == FLUID)?MassFluid:MassBound;
 
                // Get the velocity of the particle b
                Point<3,double> vb = vd.getProp<velocity>(b);
 
                // Get the pressure and density of particle b
                double Pb = vd.getProp<Pressure>(b);
                double rhob = vd.getProp<rho>(b);
 
                // Get the distance between p and q
                Point<3,double> dr = xa - xb;
                // take the norm of this vector
                double r2 = norm2(dr);
 
                // If the particles interact ...
                if (r2 < 4.0*H*H)
                {
                    // ... calculate delta rho
                    double r = sqrt(r2);
 
                    Point<3,double> dv = va - vb;
 
                    Point<3,double> DW;
                    DWab(dr,DW,r,false);
 
                    const double dot = dr.get(0)*dv.get(0) + dr.get(1)*dv.get(1) + dr.get(2)*dv.get(2);
                    const double dot_rr2 = dot/(r2+Eta2);
                    max_visc=std::max(dot_rr2,max_visc);
 
                    vd.getProp<drho>(a) += massb*(dv.get(0)*DW.get(0)+dv.get(1)*DW.get(1)+dv.get(2)*DW.get(2));
                }
 
                ++Np;
            }
        }
        else
        {
            // If it is a fluid particle calculate based on equation 1 and 2
 
            // Get an iterator over the neighborhood particles of p
            auto Np = NN.template getNNIterator<NO_CHECK>(NN.getCell(vd.getPos(a)));
 
            // For each neighborhood particle
            while (Np.isNext() == true)
            {
                // ... q
                auto b = Np.get();
 
                // Get the position xp of the particle
                Point<3,double> xb = vd.getPos(b);
 
                // if (p == q) skip this particle
                if (a.getKey() == b)    {++Np; continue;};
 
                double massb = (vd.getProp<type>(b) == FLUID)?MassFluid:MassBound;
                Point<3,double> vb = vd.getProp<velocity>(b);
                double Pb = vd.getProp<Pressure>(b);
                double rhob = vd.getProp<rho>(b);
 
                // Get the distance between p and q
                Point<3,double> dr = xa - xb;
                // take the norm of this vector
                double r2 = norm2(dr);
 
                // if they interact
                if (r2 < 4.0*H*H)
                {
                    double r = sqrt(r2);
 
                    Point<3,double> v_rel = va - vb;
 
                    Point<3,double> DW;
                    DWab(dr,DW,r,false);
 
                    double factor = - massb*((vd.getProp<Pressure>(a) + vd.getProp<Pressure>(b)) / (rhoa * rhob) + Tensile(r,rhoa,rhob,Pa,Pb) + Pi(dr,r2,v_rel,rhoa,rhob,massb,max_visc));
 
                    vd.getProp<force>(a)[0] += factor * DW.get(0);
                    vd.getProp<force>(a)[1] += factor * DW.get(1);
                    vd.getProp<force>(a)[2] += factor * DW.get(2);
 
                    vd.getProp<drho>(a) += massb*(v_rel.get(0)*DW.get(0)+v_rel.get(1)*DW.get(1)+v_rel.get(2)*DW.get(2));
                }
 
                ++Np;
            }
        }
 
        ++part;
    }
}
 
void max_acceleration_and_velocity(particles & vd, double & max_acc, double & max_vel)
{
    // Calculate the maximum acceleration
    auto part = vd.getDomainIterator();
 
    while (part.isNext())
    {
        auto a = part.get();
 
        Point<3,double> acc(vd.getProp<force>(a));
        double acc2 = norm2(acc);
 
        Point<3,double> vel(vd.getProp<velocity>(a));
        double vel2 = norm2(vel);
 
        if (vel2 >= max_vel)
            max_vel = vel2;
 
        if (acc2 >= max_acc)
            max_acc = acc2;
 
        ++part;
    }
    max_acc = sqrt(max_acc);
    max_vel = sqrt(max_vel);
 
    Vcluster<> & v_cl = create_vcluster();
    v_cl.max(max_acc);
    v_cl.max(max_vel);
    v_cl.execute();
}
 
double calc_deltaT(particles & vd, double ViscDtMax)
{
    double Maxacc = 0.0;
    double Maxvel = 0.0;
    max_acceleration_and_velocity(vd,Maxacc,Maxvel);
 
    //-dt1 depends on force per unit mass.
    const double dt_f = (Maxacc)?sqrt(H/Maxacc):std::numeric_limits<int>::max();
 
    //-dt2 combines the Courant and the viscous time-step controls.
    const double dt_cv = H/(std::max(cbar,Maxvel*10.) + H*ViscDtMax);
 
    //-dt new value of time step.
    double dt=double(CFLnumber)*std::min(dt_f,dt_cv);
    if(dt<double(DtMin))
        dt=double(DtMin);
 
    return dt;
}
 
openfpm::vector<size_t> to_remove;
 
size_t cnt = 0;
 
void verlet_int(particles & vd, double dt)
{
    // list of the particle to remove
    to_remove.clear();
 
    // particle iterator
    auto part = vd.getDomainIterator();
 
    double dt205 = dt*dt*0.5;
    double dt2 = dt*2.0;
 
    // For each particle ...
    while (part.isNext())
    {
        // ... a
        auto a = part.get();
 
        // if the particle is boundary
        if (vd.template getProp<type>(a) == BOUNDARY)
        {
            // Update rho
            double rhop = vd.template getProp<rho>(a);
 
            // Update only the density
            vd.template getProp<velocity>(a)[0] = 0.0;
            vd.template getProp<velocity>(a)[1] = 0.0;
            vd.template getProp<velocity>(a)[2] = 0.0;
            double rhonew = vd.template getProp<rho_prev>(a) + dt2*vd.template getProp<drho>(a);
            vd.template getProp<rho>(a) = (rhonew < rho_zero)?rho_zero:rhonew;
 
            vd.template getProp<rho_prev>(a) = rhop;
 
            ++part;
            continue;
        }
 
        //-Calculate displacement and update position / Calcula desplazamiento y actualiza posicion.
        double dx = vd.template getProp<velocity>(a)[0]*dt + vd.template getProp<force>(a)[0]*dt205;
        double dy = vd.template getProp<velocity>(a)[1]*dt + vd.template getProp<force>(a)[1]*dt205;
        double dz = vd.template getProp<velocity>(a)[2]*dt + vd.template getProp<force>(a)[2]*dt205;
 
        vd.getPos(a)[0] += dx;
        vd.getPos(a)[1] += dy;
        vd.getPos(a)[2] += dz;
 
        double velX = vd.template getProp<velocity>(a)[0];
        double velY = vd.template getProp<velocity>(a)[1];
        double velZ = vd.template getProp<velocity>(a)[2];
        double rhop = vd.template getProp<rho>(a);
 
        vd.template getProp<velocity>(a)[0] = vd.template getProp<velocity_prev>(a)[0] + vd.template getProp<force>(a)[0]*dt2;
        vd.template getProp<velocity>(a)[1] = vd.template getProp<velocity_prev>(a)[1] + vd.template getProp<force>(a)[1]*dt2;
        vd.template getProp<velocity>(a)[2] = vd.template getProp<velocity_prev>(a)[2] + vd.template getProp<force>(a)[2]*dt2;
        vd.template getProp<rho>(a) = vd.template getProp<rho_prev>(a) + dt2*vd.template getProp<drho>(a);
 
        // Check if the particle go out of range in space and in density
        if (vd.getPos(a)[0] <  0.000263878 || vd.getPos(a)[1] < 0.000263878 || vd.getPos(a)[2] < 0.000263878 ||
            vd.getPos(a)[0] >  0.000263878+1.59947 || vd.getPos(a)[1] > 0.000263878+0.672972 || vd.getPos(a)[2] > 0.000263878+0.903944 ||
            vd.template getProp<rho>(a) < RhoMin || vd.template getProp<rho>(a) > RhoMax)
        {
                       to_remove.add(a.getKey());
        }
 
        vd.template getProp<velocity_prev>(a)[0] = velX;
        vd.template getProp<velocity_prev>(a)[1] = velY;
        vd.template getProp<velocity_prev>(a)[2] = velZ;
        vd.template getProp<rho_prev>(a) = rhop;
 
        ++part;
    }
 
    // remove the particles
    vd.remove(to_remove,0);
 
    // increment the iteration counter
    cnt++;
}
 
void euler_int(particles & vd, double dt)
{
    // list of the particle to remove
    to_remove.clear();
 
    // particle iterator
    auto part = vd.getDomainIterator();
 
    double dt205 = dt*dt*0.5;
    double dt2 = dt*2.0;
 
    // For each particle ...
    while (part.isNext())
    {
        // ... a
        auto a = part.get();
 
        // if the particle is boundary
        if (vd.template getProp<type>(a) == BOUNDARY)
        {
            // Update rho
            double rhop = vd.template getProp<rho>(a);
 
            // Update only the density
            vd.template getProp<velocity>(a)[0] = 0.0;
            vd.template getProp<velocity>(a)[1] = 0.0;
            vd.template getProp<velocity>(a)[2] = 0.0;
            double rhonew = vd.template getProp<rho>(a) + dt*vd.template getProp<drho>(a);
            vd.template getProp<rho>(a) = (rhonew < rho_zero)?rho_zero:rhonew;
 
            vd.template getProp<rho_prev>(a) = rhop;
 
            ++part;
            continue;
        }
 
        //-Calculate displacement and update position / Calcula desplazamiento y actualiza posicion.
        double dx = vd.template getProp<velocity>(a)[0]*dt + vd.template getProp<force>(a)[0]*dt205;
        double dy = vd.template getProp<velocity>(a)[1]*dt + vd.template getProp<force>(a)[1]*dt205;
        double dz = vd.template getProp<velocity>(a)[2]*dt + vd.template getProp<force>(a)[2]*dt205;
 
        vd.getPos(a)[0] += dx;
        vd.getPos(a)[1] += dy;
        vd.getPos(a)[2] += dz;
 
        double velX = vd.template getProp<velocity>(a)[0];
        double velY = vd.template getProp<velocity>(a)[1];
        double velZ = vd.template getProp<velocity>(a)[2];
        double rhop = vd.template getProp<rho>(a);
 
        vd.template getProp<velocity>(a)[0] = vd.template getProp<velocity>(a)[0] + vd.template getProp<force>(a)[0]*dt;
        vd.template getProp<velocity>(a)[1] = vd.template getProp<velocity>(a)[1] + vd.template getProp<force>(a)[1]*dt;
        vd.template getProp<velocity>(a)[2] = vd.template getProp<velocity>(a)[2] + vd.template getProp<force>(a)[2]*dt;
        vd.template getProp<rho>(a) = vd.template getProp<rho>(a) + dt*vd.template getProp<drho>(a);
 
        // Check if the particle go out of range in space and in density
        if (vd.getPos(a)[0] <  0.000263878 || vd.getPos(a)[1] < 0.000263878 || vd.getPos(a)[2] < 0.000263878 ||
            vd.getPos(a)[0] >  0.000263878+1.59947 || vd.getPos(a)[1] > 0.000263878+0.672972 || vd.getPos(a)[2] > 0.000263878+0.903944 ||
            vd.template getProp<rho>(a) < RhoMin || vd.template getProp<rho>(a) > RhoMax)
        {
                       to_remove.add(a.getKey());
        }
 
        vd.template getProp<velocity_prev>(a)[0] = velX;
        vd.template getProp<velocity_prev>(a)[1] = velY;
        vd.template getProp<velocity_prev>(a)[2] = velZ;
        vd.template getProp<rho_prev>(a) = rhop;
 
        ++part;
    }
 
    // remove the particles
    vd.remove(to_remove,0);
 
    // increment the iteration counter
    cnt++;
}
 
template<typename Vector, typename CellList>
inline void sensor_pressure(Vector & vd,
                            CellList & NN,
                            openfpm::vector<openfpm::vector<double>> & press_t,
                            openfpm::vector<Point<3,double>> & probes)
{
    Vcluster<> & v_cl = create_vcluster();
 
    press_t.add();
 
    for (size_t i = 0 ; i < probes.size() ; i++)
    {
        float press_tmp = 0.0f;
        float tot_ker = 0.0;
 
        // if the probe is inside the processor domain
        if (vd.getDecomposition().isLocal(probes.get(i)) == true)
        {
            // Get the position of the probe i
            Point<3,double> xp = probes.get(i);
 
            // get the iterator over the neighbohood particles of the probes position
            auto itg = NN.template getNNIterator<NO_CHECK>(NN.getCell(probes.get(i)));
            while (itg.isNext())
            {
                auto q = itg.get();
 
                // Only the fluid particles are importants
                if (vd.template getProp<type>(q) != FLUID)
                {
                    ++itg;
                    continue;
                }
 
                // Get the position of the neighborhood particle q
                Point<3,double> xq = vd.getPos(q);
 
                // Calculate the contribution of the particle to the pressure
                // of the probe
                double r = sqrt(norm2(xp - xq));
 
                double ker = Wab(r) * (MassFluid / rho_zero);
 
                // Also keep track of the calculation of the summed
                // kernel
                tot_ker += ker;
 
                // Add the total pressure contribution
                press_tmp += vd.template getProp<Pressure>(q) * ker;
 
                // next neighborhood particle
                ++itg;
            }
 
            // We calculate the pressure normalizing the
            // sum over all kernels
            if (tot_ker == 0.0)
                press_tmp = 0.0;
            else
                press_tmp = 1.0 / tot_ker * press_tmp;
 
        }
 
        // This is not necessary in principle, but if you
        // want to make all processor aware of the history of the calculated
        // pressure we have to execute this
        v_cl.sum(press_tmp);
        v_cl.execute();
 
        // We add the calculated pressure into the history
        press_t.last().add(press_tmp);
    }
}
 
int main(int argc, char* argv[])
{
 
    // initialize the library
    openfpm_init(&argc,&argv);
 
    // It contain for each time-step the value detected by the probes
    openfpm::vector<openfpm::vector<double>> press_t;
    openfpm::vector<Point<3,double>> probes;
 
    probes.add({0.8779,0.3,0.02});
    probes.add({0.754,0.31,0.02});
 
    // Here we define our domain a 2D box with internals from 0 to 1.0 for x and y
    Box<3,double> domain({-0.05,-0.05,-0.05},{1.7010,0.7065,0.5025});
    size_t sz[3] = {207,90,66};
 
    // Fill W_dap
    W_dap = 1.0/Wab(H/1.5);
 
    // Here we define the boundary conditions of our problem
    size_t bc[3]={NON_PERIODIC,NON_PERIODIC,NON_PERIODIC};
 
    // extended boundary around the domain, and the processor domain
    Ghost<3,double> g(2*H);
    
 
 
    particles vd(0,domain,bc,g,DEC_GRAN(512));
 
 
 
    // You can ignore all these dp/2.0 is a trick to reach the same initialization
    // of Dual-SPH that use a different criteria to draw particles
    Box<3,double> fluid_box({dp/2.0,dp/2.0,dp/2.0},{0.4+dp/2.0,0.67-dp/2.0,0.3+dp/2.0});
 
    // return an iterator to the fluid particles to add to vd
    auto fluid_it = DrawParticles::DrawBox(vd,sz,domain,fluid_box);
 
    // here we fill some of the constants needed by the simulation
    max_fluid_height = fluid_it.getBoxMargins().getHigh(2);
    h_swl = fluid_it.getBoxMargins().getHigh(2) - fluid_it.getBoxMargins().getLow(2);
    B = (coeff_sound)*(coeff_sound)*gravity*h_swl*rho_zero / gamma_;
    cbar = coeff_sound * sqrt(gravity * h_swl);
 
    // for each particle inside the fluid box ...
    while (fluid_it.isNext())
    {
        // ... add a particle ...
        vd.add();
 
        // ... and set it position ...
        vd.getLastPos()[0] = fluid_it.get().get(0);
        vd.getLastPos()[1] = fluid_it.get().get(1);
        vd.getLastPos()[2] = fluid_it.get().get(2);
 
        // and its type.
        vd.template getLastProp<type>() = FLUID;
 
        // We also initialize the density of the particle and the hydro-static pressure given by
        //
        // rho_zero*g*h = P
        //
        // rho_p = (P/B + 1)^(1/Gamma) * rho_zero
        //
 
        vd.template getLastProp<Pressure>() = rho_zero * gravity *  (max_fluid_height - fluid_it.get().get(2));
 
        vd.template getLastProp<rho>() = pow(vd.template getLastProp<Pressure>() / B + 1, 1.0/gamma_) * rho_zero;
        vd.template getLastProp<rho_prev>() = vd.template getLastProp<rho>();
        vd.template getLastProp<velocity>()[0] = 0.0;
        vd.template getLastProp<velocity>()[1] = 0.0;
        vd.template getLastProp<velocity>()[2] = 0.0;
 
        vd.template getLastProp<velocity_prev>()[0] = 0.0;
        vd.template getLastProp<velocity_prev>()[1] = 0.0;
        vd.template getLastProp<velocity_prev>()[2] = 0.0;
 
        // next fluid particle
        ++fluid_it;
    }
 
 
 
    // Recipient
    Box<3,double> recipient1({0.0,0.0,0.0},{1.6+dp/2.0,0.67+dp/2.0,0.4+dp/2.0});
    Box<3,double> recipient2({dp,dp,dp},{1.6-dp/2.0,0.67-dp/2.0,0.4+dp/2.0});
 
    Box<3,double> obstacle1({0.9,0.24-dp/2.0,0.0},{1.02+dp/2.0,0.36,0.45+dp/2.0});
    Box<3,double> obstacle2({0.9+dp,0.24+dp/2.0,0.0},{1.02-dp/2.0,0.36-dp,0.45-dp/2.0});
    Box<3,double> obstacle3({0.9+dp,0.24,0.0},{1.02,0.36,0.45});
 
    openfpm::vector<Box<3,double>> holes;
    holes.add(recipient2);
    holes.add(obstacle1);
    auto bound_box = DrawParticles::DrawSkin(vd,sz,domain,holes,recipient1);
 
    while (bound_box.isNext())
    {
        vd.add();
 
        vd.getLastPos()[0] = bound_box.get().get(0);
        vd.getLastPos()[1] = bound_box.get().get(1);
        vd.getLastPos()[2] = bound_box.get().get(2);
 
        vd.template getLastProp<type>() = BOUNDARY;
        vd.template getLastProp<rho>() = rho_zero;
        vd.template getLastProp<rho_prev>() = rho_zero;
        vd.template getLastProp<velocity>()[0] = 0.0;
        vd.template getLastProp<velocity>()[1] = 0.0;
        vd.template getLastProp<velocity>()[2] = 0.0;
 
        vd.template getLastProp<velocity_prev>()[0] = 0.0;
        vd.template getLastProp<velocity_prev>()[1] = 0.0;
        vd.template getLastProp<velocity_prev>()[2] = 0.0;
 
        ++bound_box;
    }
 
 
 
    auto obstacle_box = DrawParticles::DrawSkin(vd,sz,domain,obstacle2,obstacle1);
 
    while (obstacle_box.isNext())
    {
        vd.add();
 
        vd.getLastPos()[0] = obstacle_box.get().get(0);
        vd.getLastPos()[1] = obstacle_box.get().get(1);
        vd.getLastPos()[2] = obstacle_box.get().get(2);
 
        vd.template getLastProp<type>() = BOUNDARY;
        vd.template getLastProp<rho>() = rho_zero;
        vd.template getLastProp<rho_prev>() = rho_zero;
        vd.template getLastProp<velocity>()[0] = 0.0;
        vd.template getLastProp<velocity>()[1] = 0.0;
        vd.template getLastProp<velocity>()[2] = 0.0;
 
        vd.template getLastProp<velocity_prev>()[0] = 0.0;
        vd.template getLastProp<velocity_prev>()[1] = 0.0;
        vd.template getLastProp<velocity_prev>()[2] = 0.0;
 
        ++obstacle_box;
    }
 
    vd.map();
 
 
 
    // Now that we fill the vector with particles
    ModelCustom md;
 
    vd.addComputationCosts(md);
    vd.getDecomposition().decompose();
    vd.map();
 
 
    vd.ghost_get<type,rho,Pressure,velocity>();
 
    auto NN = vd.getCellList(2*H);
 
    // Evolve
 
 
    size_t write = 0;
    size_t it = 0;
    size_t it_reb = 0;
    double t = 0.0;
    while (t <= t_end)
    {
        Vcluster<> & v_cl = create_vcluster();
        timer it_time;
 
        it_reb++;
        if (it_reb == 200)
        {
            vd.map();
 
            it_reb = 0;
            ModelCustom md;
            vd.addComputationCosts(md);
            vd.getDecomposition().decompose();
 
            if (v_cl.getProcessUnitID() == 0)
                std::cout << "REBALANCED " << std::endl;
        }
 
        vd.map();
 
        // Calculate pressure from the density
        EqState(vd);
 
        double max_visc = 0.0;
 
        vd.ghost_get<type,rho,Pressure,velocity>();
 
        // Calc forces
        calc_forces(vd,NN,max_visc);
 
        // Get the maximum viscosity term across processors
        v_cl.max(max_visc);
        v_cl.execute();
 
        // Calculate delta t integration
        double dt = calc_deltaT(vd,max_visc);
 
        // VerletStep or euler step
        it++;
        if (it < 40)
            verlet_int(vd,dt);
        else
        {
            euler_int(vd,dt);
            it = 0;
        }
 
        t += dt;
 
        if (write < t*100)
        {
            // sensor_pressure calculation require ghost and update cell-list
            vd.map();
            vd.ghost_get<type,rho,Pressure,velocity>();
            vd.updateCellList(NN);
 
            // calculate the pressure at the sensor points
            sensor_pressure(vd,NN,press_t,probes);
 
            vd.write_frame("Geometry",write);
            write++;
 
            if (v_cl.getProcessUnitID() == 0)
            {std::cout << "TIME: " << t << "  write " << it_time.getwct() << "   " << v_cl.getProcessUnitID() << "   " << cnt << "   Max visc: " << max_visc << std::endl;}
        }
        else
        {
            if (v_cl.getProcessUnitID() == 0)
            {std::cout << "TIME: " << t << "  " << it_time.getwct() << "   " << v_cl.getProcessUnitID() << "   " << cnt << "    Max visc: " << max_visc << std::endl;}
        }
    }
 
 
 
    openfpm_finalize();
 
 
}