Gray Scott in 3D using sparse grids optimized on CPU

Solving a gray scott-system in 3D using sparse grids optimized on CPU

This example show how to solve a Gray-Scott system in 3D using sparse grids in an optimized way

In figure is the final solution of the problem

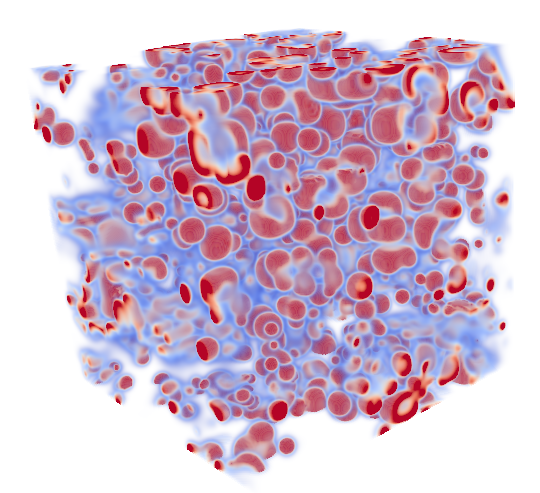
More or less this example is the adaptation of the dense example in 3D

See also

Gray Scott in 3D

This example is the same as e3_gs_gray_scott_sparse the difference is optimizing for speed.

Two optimization has been done. The first is to change the layout to struct of arrays defining the grid with

 
    sgrid_dist_soa<3, double, aggregate<double,double,double,double>> grid(sz,domain,g,bc);
 

The second is using the function conv_cross2 to calculate the right-hand-side this function can be used to do a convolution that involve points in a cross stencil like in figure that involve two properties

     *
     *
 * * x * *
     *
     *

The function accept a lambda function where the first 2 arguments are the output in form of Vc::double_v. If we use double we have to use Vc::double_v or Vc::int_v in case the property is an integer. Vc variables come from the Vc library that is now integrated in openfpm.

Vc Library *

Vc::double_v in general pack 1,2,4 doubles dependently from the fact we choose to activate no-SSE,SSE or AVX at compiler level. The arguments 3 and 4 contain the properties of two selected properties in the cross pattern given by xm xp ym yp zm zp. The last arguments is instead the mask. The mask can be accessed to check the number of existing points. For example if we have a cross stencil in 3D with stencil size = 1 than we expect 6 points. Note that the mask is an array because if Vc::double_v contain 4 doubles than the mask has 4 elements accessed with the array operator []. The call cross_conv2 also accept template parameters the first two indicate the source porperties, the other two are the destination properties. While the last is the extension of the stencil. In this case we use 1.

The lambda function is defined as

 
 
        auto func = [uFactor,vFactor,deltaT,F,K](Vc::double_v & u_out,Vc::double_v & v_out,
                                                   Vc::double_v & u,Vc::double_v & v,
                                                   cross_stencil_v<double> & uc,cross_stencil_v<double> & vc,
                                                   unsigned char * mask){
 
                u_out = u + uFactor *(uc.xm + uc.xp +
                                                                                                 uc.ym + uc.yp +
                                                                                                 uc.zm + uc.zp - 6.0*u) - deltaT * u*v*v
                                                                                               - deltaT * F * (u - 1.0);
 
                v_out = v + vFactor *(vc.xm + vc.xp +
                                                                                                 vc.ym + vc.yp +
                                                                                                 vc.zm + vc.zp - 6.0*v) + deltaT * u*v*v
                                                                                               - deltaT * (F+K) * v;
                                            };
 

and used in the body loop

 
        if (i % 2 == 0)
        {
 
            timer ts;
            ts.start();
            grid.conv_cross2<U,V,U_next,V_next,1>({0,0,0},{(long int)sz[0]-1,(long int)sz[1]-1,(long int)sz[2]-1},func);
            ts.stop();
            std::cout << ts.getwct() << std::endl;
    
            // After copy we synchronize again the ghost part U and V
            grid.ghost_get<U_next,V_next>();
        }
        else
        {
            grid.conv_cross2<U_next,V_next,U,V,1>({0,0,0},{(long int)sz[0]-1,(long int)sz[1]-1,(long int)sz[2]-1},func);
 
            // After copy we synchronize again the ghost part U and V
            grid.ghost_get<U,V>();
        }
 

To note that instead of copy we split the properties where we are acting at every iteration

Finalize

Deinitialize the library

 
    openfpm_finalize();
 

Full code

Solving a gray scott-system in 3D using sparse grids optimized on CPU

This example show how to solve a Gray-Scott system in 3D using sparse grids in an optimized way

In figure is the final solution of the problem

More or less this example is the adaptation of the dense example in 3D

See also

Gray Scott in 3D

This example is the same as e3_gs_gray_scott_sparse the difference is optimizing for speed.

Two optimization has been done. The first is to change the layout to struct of arrays defining the grid with

The second is using the function conv_cross2 to calculate the right-hand-side this function can be used to do a convolution that involve points in a cross stencil like in figure that involve two properties

     *
     *
 * * x * *
     *
     *

The function accept a lambda function where the first 2 arguments are the output in form of Vc::double_v. If we use float we have to use Vc::float_v or Vc::int_v in case the property is an integer. Vc variables come from the Vc library that is now integrated in openfpm.

Vc Library *

Vc::double_v in general pack 1,2,4 doubles dependently from the fact we choose to activate no-SSE,SSE or AVX at compiler level. The arguments 3 and 4 contain the properties of two selected properties in the cross pattern given by xm xp ym yp zm zp. The last arguments is instead the mask. The mask can be accessed to check the number of existing points. For example if we have a cross stencil in 3D with stencil size = 1 than we expect 6 points. Note that the mask is an array because if Vc::double_v contain 4 doubles than the mask has 4 elements accessed with the array operator []. The call cross_conv2 also accept template parameters the first two indicate the source porperties, the other two are the destination properties. While the last is the extension of the stencil. In this case we use 1.

The lambda function is defined as

and used in the body loop

To note that instead of copy we split the properties where we are acting at every iteration

Finalize

Deinitialize the library