This example show how to solve a Gray-Scott system in 3D using sparse grids on gpu
In figure is the final solution of the problem
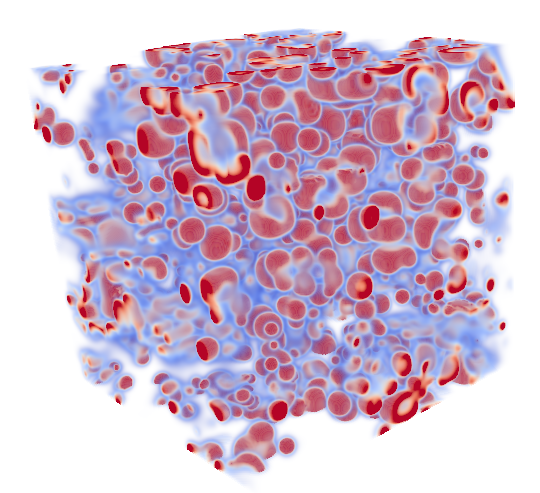
More or less this example is the adaptation of the dense example in 3D
On gpu we can add points using the function addPoints this function take 2 lamda functions the first take 3 arguments (in 3D) i,j,k these are the global coordinates for a point. We can return either true either false. In case of true the point is created in case of false the point is not inserted. The second lamda is instead used to initialize the point inserted. The arguments of the second lambda are the data argument we use to initialize the point and the global coordinates i,j,k
After we add the points we have to flush the added points. This us achieved using the function flush the template parameters indicate how we have to act on the points. Consider infact we are adding points already exist ... do we have to add it using the max or the min. FLUSH_ON_DEVICE say instead that the operation is performed using the GPU
The function can also called with a specified range
to calculate the right-hand-side we use the function conv2 this function can be used to do a convolution that involve two properties
The function accept a lambda function where the first 2 arguments are the output of the same type of the two property choosen.
The arguments 3 and 4 contain the properties of two selected properties. while i,j,k are the coordinates we have to calculate the convolution. The call conv2 also accept template parameters the first two indicate the source porperties, the other two are the destination properties. While the last is the extension of the stencil. In this case we use 1.
The lambda function is defined as
and used in the body loop
This example show how to solve a Gray-Scott system in 3D using sparse grids on gpu
In figure is the final solution of the problem

More or less this example is the adaptation of the dense example in 3D
On gpu we can add points using the function addPoints this function take 2 lamda functions the first take 3 arguments (in 3D) i,j,k these are the global coordinates for a point. We can return either true either false. In case of true the point is created in case of false the point is not inserted. The second lamda is instead used to initialize the point inserted. The arguments of the second lambda are the data argument we use to initialize the point and the global coordinates i,j,k
After we add the points we have to flush the added points. This us achieved using the function flush the template parameters indicate how we have to act on the points. Consider infact we are adding points already exist ... do we have to add it using the max or the min. FLUSH_ON_DEVICE say instead that the operation is performed using the GPU
The function can also called with a specified range
to calculate the right-hand-side we use the function conv2 this function can be used to do a convolution that involve two properties
The function accept a lambda function where the first 2 arguments are the output of the same type of the two property choosen.
The arguments 3 and 4 contain the properties of two selected properties. while i,j,k are the coordinates we have to calculate the convolution. The call conv2 also accept template parameters the first two indicate the source porperties, the other two are the destination properties. While the last is the extension of the stencil. In this case we use 1.
The lambda function is defined as
and used in the body loop
This example show how to solve a Gray-Scott system in 3D using sparse grids on gpu
In figure is the final solution of the problem

More or less this example is the adaptation of the dense example in 3D
On gpu we can add points using the function addPoints this function take 2 lamda functions the first take 3 arguments (in 3D) i,j,k these are the global coordinates for a point. We can return either true either false. In case of true the point is created in case of false the point is not inserted. The second lamda is instead used to initialize the point inserted. The arguments of the second lambda are the data argument we use to initialize the point and the global coordinates i,j,k
After we add the points we have to flush the added points. This us achieved using the function flush the template parameters indicate how we have to act on the points. Consider infact we are adding points already exist ... do we have to add it using the max or the min. FLUSH_ON_DEVICE say instead that the operation is performed using the GPU
The function can also called with a specified range
to calculate the right-hand-side we use the function conv2 this function can be used to do a convolution that involve two properties
The function accept a lambda function where the first 2 arguments are the output of the same type of the two property choosen.
The arguments 3 and 4 contain the properties of two selected properties. while i,j,k are the coordinates we have to calculate the convolution. The call conv2 also accept template parameters the first two indicate the source porperties, the other two are the destination properties. While the last is the extension of the stencil. In this case we use 1.
The lambda function is defined as
and used in the body loop