Gray Scott in 3D using sparse grids with complex geometry

Table of Contents

• Solving a gray scott-system in 3D using Sparse grids
• Initialization
• Boundary conditions

Solving a gray scott-system in 3D using Sparse grids

This example show how to solve a Gray-Scott system in 3D using sparse grids. In this example we will construct a complex geometry

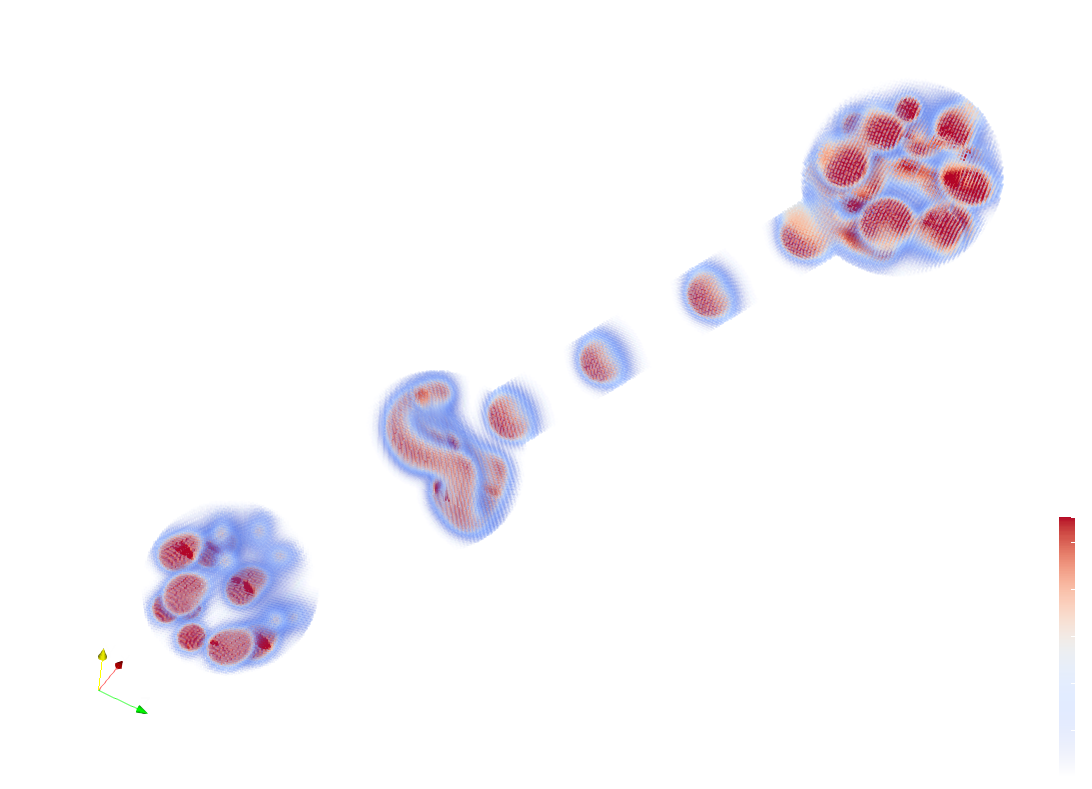
In figure is the final solution of the problem

This example follow the gray scott 3d sparse with the addition that the initialization is completely different to create a complex geometry initialization

We recall here the main differences between sparse and dense.

• Get function return now constant values, so cannot be used to get values, a get in write is an insert a get on a point position that has not been inserted yet return the background value
• Insert function create/overwrite the points value
• getDomainIterator return an iterator on the existing points
• getGridIterator return an iterator on the dense version of the grid

Initialization

The initialization involve the creation of 3 sphere and one cylinder channel connecting them in order to do it we create an iterator over the grid (inserted and not inserted) point with getGridIterator

 
    auto it = Old.getGridIterator();
    Point<3,double> p1;
    Point<3,double> p2;
    Point<3,double> p3;
 
    // Shere1
    for (int i = 0 ; i < 3 ; i++)
    {p1.get(i) = 2.0;}
 
        // Shere2
        for (int i = 0 ; i < 3 ; i++)
        {p2.get(i) = 1.0;}
 
        // Shere3
        for (int i = 0 ; i < 3 ; i++)
        {p3.get(i) = 0.5;}
 
    Sphere<3,double> sph1(p1,0.3);
    Sphere<3,double> sph2(p2,0.3);
    Sphere<3,double> sph3(p3,0.3);
 
    Point<3,double> u({1.0,1.0,1.0});
    Box<3,double> channel_box(p3,p1);
 
    while (it.isNext())
    {
        // Get the local grid key
        auto key = it.get_dist();
        auto keyg = it.get();
 
        Point<3,double> pc;
        Point<3,double> vp;
 
        for (int i = 0 ; i < 3 ; i++)
            {pc.get(i) = keyg.get(i) * it.getSpacing(i);}
 
                // calculate the distance from the diagonal
                vp.get(0) = pc.get(1)*u.get(2) - pc.get(2)*u.get(1);
                vp.get(1) = pc.get(2)*u.get(0) - pc.get(0)*u.get(2);
                vp.get(2) = pc.get(0)*u.get(1) - pc.get(1)*u.get(0);
 
                double distance = vp.norm() / sqrt(3);
 
        // Check if the point is in the first sphere
        if (sph1.isInside(pc) || sph2.isInside(pc) || sph3.isInside(pc) || (distance < 0.1 && channel_box.isInside(pc)) )
        {
            // Old values U and V
            Old.template insert<U>(key) = 1.0;
            Old.template insert<V>(key) = 0.0;
 
            // Old values U and V
            New.template insert<U>(key) = 0.0;
            New.template insert<V>(key) = 0.0;
        }
 
        ++it;
    }
 

After creating the domain we make a perturbation in the up sphere

 
    long int x_start = Old.size(0)*1.95f/domain.getHigh(0);
    long int y_start = Old.size(1)*1.95f/domain.getHigh(1);
    long int z_start = Old.size(1)*1.95f/domain.getHigh(2);
 
    long int x_stop = Old.size(0)*2.05f/domain.getHigh(0);
    long int y_stop = Old.size(1)*2.05f/domain.getHigh(1);
    long int z_stop = Old.size(1)*2.05f/domain.getHigh(2);
 
    grid_key_dx<3> start({x_start,y_start,z_start});
    grid_key_dx<3> stop ({x_stop,y_stop,z_stop});
    auto it_init = Old.getGridIterator(start,stop);
 
    while (it_init.isNext())
    {
        auto key = it_init.get_dist();
 
                Old.template insert<U>(key) = 0.5 + (((double)std::rand())/RAND_MAX -0.5)/10.0;
                Old.template insert<V>(key) = 0.25 + (((double)std::rand())/RAND_MAX -0.5)/20.0;
 
        ++it_init;
    }
 

Boundary conditions

For this example we use mirror on direction X Y Z If the point is missing. If the point is missing in both direction than the second derivative is considered zero

 
            double LapU = 0.0;
            double LapV = 0.0;
 
            // Mirror z
 
            if (Old.existPoint(mz) == true)
            {
                LapU += Old.get<U>(mz);
                LapV += Old.get<V>(mz);
            }
            else if (Old.existPoint(pz) == true)
            {
                LapU += Old.get<U>(pz);
                LapV += Old.get<V>(pz);
            }
            else
            {
                LapU += Old.get<U>(Cp);
                LapV += Old.get<V>(Cp);
            }
 
            if (Old.existPoint(pz) == true)
            {
                LapU += Old.get<U>(pz);
                LapV += Old.get<V>(pz);
            }
            else if (Old.existPoint(mz) == true)
            {
                LapU+= Old.get<U>(mz);
                LapV += Old.get<V>(mz);
            }
            else
            {
                LapU+= Old.get<U>(Cp);
                LapV += Old.get<V>(Cp);
            }
 
 
            // Mirror y
 
            if (Old.existPoint(my) == true)
            {
                    LapU += Old.get<U>(my);
                    LapV += Old.get<V>(my);
            }
            else if (Old.existPoint(py) == true)
            {
                    LapU += Old.get<U>(py);
                    LapV += Old.get<V>(py);
            }
            else
            {
                LapU+= Old.get<U>(Cp);
                LapV += Old.get<V>(Cp);
            }
 
            if (Old.existPoint(py) == true)
            {
                    LapU += Old.get<U>(py);
                    LapV += Old.get<V>(py);
            }
            else if (Old.existPoint(my) == true)
            {
                    LapU+= Old.get<U>(my);
                    LapV += Old.get<V>(my);
            }
            else
            {
                LapU+= Old.get<U>(Cp);
                LapV += Old.get<V>(Cp);
            }
 
            // Mirror x
 
            if (Old.existPoint(mx) == true)
            {
                    LapU += Old.get<U>(mx);
                    LapV += Old.get<V>(mx);
            }
            else if (Old.existPoint(px) == true)
            {
                    LapU += Old.get<U>(px);
                    LapV += Old.get<V>(px);
            }
            else
            {
                LapU+= Old.get<U>(Cp);
                LapV += Old.get<V>(Cp);
            }
 
            if (Old.existPoint(px) == true)
            {
                    LapU += Old.get<U>(px);
                    LapV += Old.get<V>(px);
            }
            else if (Old.existPoint(mx) == true)
            {
                    LapU+= Old.get<U>(mx);
                    LapV += Old.get<V>(mx);
            }
            else
            {
                LapU+= Old.get<U>(Cp);
                LapV += Old.get<V>(Cp);
            }
 
            LapU -= 6.0*Old.get<U>(Cp);
            LapV -= 6.0*Old.get<V>(Cp);