Molecular Dynamic with Lennard-Jones potential on GPU (Optimized)

In this optimized version of the example Molecular Dynamic with Lennard-Jones potential on GPU, we operate two optimization:

We make the access coalesced
We use half radius cell-list spacing

Coalesced access

In GPU to get the maximum performance it is very important to access in a coalesced way. Access in a coalesced way mean that if thread 1 access adress 0x000 thread 2 (in the same Streaming Multiprocessors) should ideally access 0x004 or more in general an adress in the same cache line. Another factor that contribute to speed is to overall restrict the threads in the same SM should to possibly work on a limited number of caches lines so that the L1 cache of each SM could optimally speed up the access to global memory.

Unfortunately particles by nature can be randomly distributed in space and memory, and reach the ideal situation in the case of neighborhood access of the particles can be challenging. Suppose that thread 1 take particle 0 and thread 2 take particle 1, but 0 and 1 are far in space the neighborhood of 0 does not overlap the neighborhood of 1. This mean that most probably the access of the neighborhood of 0 will be scattered in memory and the same for 1, having an extremely low probability that 2 thread in the SM hit the same cache line and increasing the number of cache lines the SM has to retrieve. On the other hand if we reorder the particle in memory by their spatial position using a cell list like in figure.


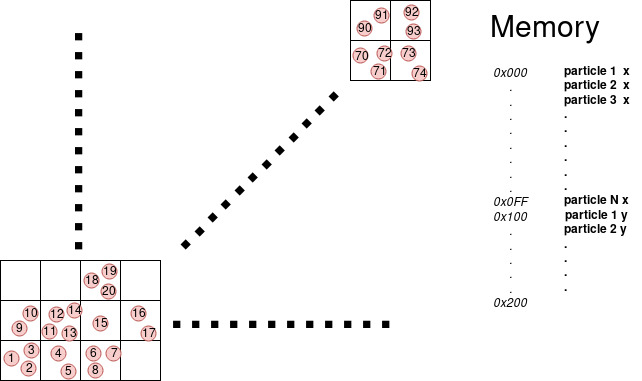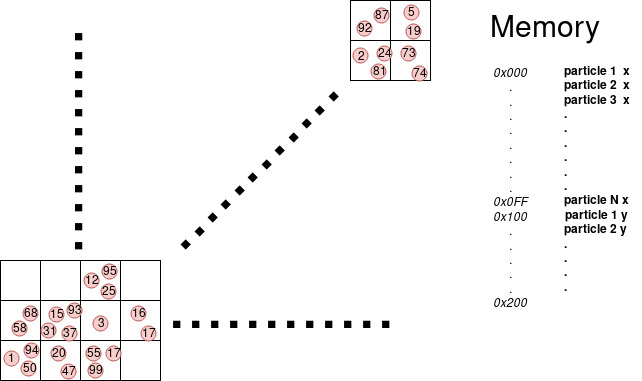Fig1: Sorted vector	Fig2: Unsorted vector

We can see that now the neighborhood of particle 0 and particle 1 overlap increasing that chance of cache hit, additionally if all particles processed by one SM stay in one cell or few neighborhood cell, the number of cache line that an SM has to read is reduced, with a significant speed-up.

In OpenFPM get a Cell-list produce a re-ordered version of the original vector by default. It is possible to offload the sorted version vector_dist_gpu instead of the normal one using the function toKernel_sorted() instead of the function toKernel .

 
    CUDA_LAUNCH(calc_force_gpu,it2,vd.toKernel_sorted(),NN.toKernel(),sigma12,sigma6,r_cut2);
 

The rest remain mainly the same, with the expectation, that we now use the macro GET_PARTICLE_SORT. This macro is similar to GET_PARTICLE but with a substantial difference. While in the normal unsorted vector particles in the ghost area are always added at the end in the sorted one domain + ghost are reordered, and there is not a clear separation between them. This mean that we need a list of all the domain particles, if we want iterate cross them. GET_PARTICLE_SORT use a list to convert thread index to domain particle index. Additionally when we get a neighborhood iterator from the Cell-list we must use \bget_sorted_indexinstead of \bget

 
        // ... q
        auto q = Np.get_sort();

After we launched the kernel all the data are written in the sorted vector. In order to merge back the data to the unsorted one we have to use the function vd.merge_sort<force>(NN) . Where vd is the vector_dist_gpu where we want to merge the data from sorted to non sorted. force is the property we want to merge and NN is the Cell-list that produced the sorted distribution.

 
    vd.merge_sort<force>(NN);
 

Note: it is possible to launch multiple kernel on the sorted version, but consider that at some point the data must be merged back because functions like map and ghost_get work on the unsorted version

Half radius cell-list spacing

Using Cell-lists with spacing equal to the radius in general require to fetch all the 9 cells in 2D and 27 cells in 3D. All the particles in such cells include particles within radius r and others more distant than r. This mean that we have to filter the particles checking the radius. It is possible to filter further more the particles using finer cell-list cells. Suppose that you use cell-lists with spacing half of the radius. we just the to check the 25 cells in 2D and the 125 cells in 3D. While we have more cells the overall volume spanned by the 25/125 cells is just a fraction. In fact the surface of the 25 cells is given by

\( (5\frac{h}{2})^2 = \frac{25}{4} h^2 \) \( (5\frac{h}{2})^3 = \frac{125}{8} h^3 \)

while for the normal cell-list is

\( (3h)^2 = 9h^2 \) \( (3h)^3 = 27h^3 \)

This mean that the finer cell-list in order to find the neighborhood particles use an area smaller: precisely is 69% of the normal cell-list in 2D, and 57% of the normal cell-list in 3D. In particles this mean that normal cell-list return in average 45% more particles in 2D and 75% more in 3D.

Constructing an half spacing cell-list is standard. In the function getCellListGPU we specify half radius

 
    // Get the Cell list structure
    auto NN = vd.getCellListGPU(r_cut / 2.0);

while to use it, instead of the getNNIteratorBox we use

Note: getNNIteratorBox has a template parameter (default = 2) that indicate how many neighborhood cell the NN iterator has to span. For example getNNIteratorBox<1> is the standard 9/27 neighborhood cell-list.getNNIteratorBox<2> is the 25/125 neighborhood and so on.

Table of Contents

Molecular Dynamic with Lennard-Jones potential on GPU (Optimized)

Coalesced access

Half radius cell-list spacing